ap scert 10th class Maths Lesson 8 Introduction to Trigonometry

Chapters

Solutions
Important Question
Question Papers / Notes Download
Videos

Solutions

Question 1.
In △PQR, ST is a line such that PS/SQ=PT/TR and also ∠PST = ∠PRQ.
Prove that △PQR is an isosceles triangle.

Answer:
Given : In △PQR,
PS/SQ=PT/TR and ∠PST= ∠PRQ.

R.T.P: △PQR is isosceles.
Proof: PS/SQ = PT/TR
Hence, ST ∥ QR (Converse of Basic proportionality theorem)
∠PST = ∠PQR .... (1)
(Corresponding angles for the lines ST ∥ QR)
Also, ∠PST = ∠PRQ ... (2) given
From (1) and (2),
∠PQR = ∠PRQ
i.e., PR = PQ
[∵ In a triangle sides opposite to equal angles are equal]
Hence, APQR is an isosceles triangle.

Question 2.
In the given figure, LM ∥ CM and LN ∥ CD. Prove that AMAB = ANAD.

Answer:
Given : LM ∥ CB and LN ∥ CD In △ABC, LM ∥ BC (given) Hence,

Adding ‘1’ on both sides.

From (1) and (2)
∴ AMAB = ANAD.

Question 3.
In the given figure, DE ∥ AC and DF ∥ AE. Prove that BF/FE = BE/AC.

Answer:
In △ABC, DE ∥ AC
Hence BE/EC = BD/DA .... (1)
[∵ A line drawn parallel to one side of a triangle divides the other two sides in the same ratio - Basic proportionality theorem]
Also in △ABE, DF ∥ AE
Hence BF/FE = BD/DA .... (2)
From (1) and (2), BF/FE = BE/AC Hence proved.

Question 4.
Prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side (Using Basic proportionality theorem).

Answer:

Given: In △ABC; D is the mid-point of AB.
A line ‘l’ through D, parallel to BC, meeting AC at E.
R.T.P: E is the midpoint of AC.
Proof:
DE ∥ BC (Given)
then
AD/DB=AE/EC(From Basic Proportional theorem)
Also given ‘D’ is mid point of AB.
Then AD = DB.
⇒AD/DB=DB/DB=AE/EC= 1
⇒ AE = EC
∴ ‘E’ is mid point of AC

Question 5.
Prove that a line joining the mid points of any two sides of a triangle is parallel to the third side. (Using converse of Basic proportionality theorem)

Answer:
Given: △ABC, D is the midpoint of AB and E is the midpoint of AC.
R.T.P : DE ∥ BC.
Proof:

Since D is the midpoint of AB, we have AD = DB ⇒AD/DB= 1 ……. (1)
also ‘E’ is the midpoint of AC, we have AE = EC ⇒AE/EC = 1 ……. (2)
From (1) and (2)
AD/DB=AE/EC
If a line divides any two sides of a triangle in the same ratio then it is parallel to the third side.
∴ DE ∥ BC by Basic proportionality theorem.
Hence proved.

Question 6.
In the given figure, DE ∥ OQ and DF ∥ OR. Show that EF ∥ QR.

Answer:
Given: △PQR, DE ∥ OQ; DF ∥ OR
R.T.P: EF ∥ QR
Proof:
In △POQ;
PEEQ = PDDO ……. (1)
[∵ ED ∥ QO, Basic proportionality theorem]
In △POR;PF/FR = PD/DO ……. (2) [∵ DF ∥ OR, Basic Proportionality Theorem]
From (1) and (2),
PE/EQ=PF/FR

Question 7.
In the given figure A, B and C are points on OP, OQ and OR respec¬tively such that AB ∥ PQ and AC ∥ PR. Show that BC ∥ QR.

Answer:
Given:
In △PQR, AB ∥ PQ; AC ∥ PR
R.T.P : BC ∥ QR
Proof: In △POQ; AB ∥ PQ
OA/AP=OB/BQ ……… (1)
(∵ Basic Proportional theorem)
and in △OPR, Proof: In △POQ; AB ∥ PQ
OA/AP=OC/CR ……… (2)
From (1) and (2), we can write
OB/BQ=OC/CR
Then consider above condition in △OQR then from (3) it is clear.
∴ BC ∥ QR [∵ from converse of Basic Proportionality Theorem]
Hence proved.

Question 8.
ABCD is a trapezium in which AB ∥ DC and its diagonals intersect each other at point ‘O’. Show that AO/BO = CO/DO.

Answer:
Given: In trapezium □ ABCD, AB ∥ CD. Diagonals AC, BD intersect at O.
R.T.P: AO/BO = CO/DO

Construction:
Draw a line EF passing through the point ‘O’ and parallel to CD and AB.
Proof: In △ACD, EO ∥ CD
∴AO/CO = AE/DE …….. (1)
[∵ line drawn parallel to one side of a triangle divides other two sides in the same ratio by Basic proportionality theorem]
In △ABD, EO ∥ AB
Hence, DE/AE = DO/BO
[∵ Basic proportionality theorem]
BO/DO = AE/ED …….. (2) [∵ Invertendo]
From (1) and (2),
AO/CO = BO/DO
⇒ AO/BO = CO/DO[∵ Alternendo]

Question 9.
Draw a line segment of length 7.2 cm and divide it in the ratio 5 : 3. Measure the two parts.
Answer:

Question 1.
In the given figure, ∠ADE = ∠B

i) Show that △ABC ~ △ADE
ii) If AD = 3.8 cm, AE = 3.6 cm, BE = 2.1 cm, BC = 4.2 cm, find DE.

Answer:
i) Given: △ABC and ∠ADE = ∠B
R.T.P: △ABC ~ △ADE.
Proof: In △ABC and △ADE
∠A = ∠A [∵ Common]
∠B = ∠ADE [∵ Given]
∴ ∠C = ∠AED [∵ By Angle Sum property of triangles] △ABC ~ △ADE. by AAA similarity condition.]
ii) AD = 3.8 cm, AE = 3.6 cm, BE = 2.1 cm, BC = 4.2 cm, find DE.
To find DE; △ABC ~ △ADE.
Hence,
AB/AD = BC/DE = AC/AE
[∵ Ratios of corresponding sides are equal]

Question 2.
The perimeters of two similar triangles are 30 cm and 20 cm respectively. If one side of the first triangle is 12 cm, determine the corresponding side of the second triangle.

Answer:

Given: △ABC ~ △PQR Perimeter of △ABC = 30 cm. Perimeter of △PQR = 20 cm. AB = 12 cm.

Question 3.
A girl of height 90 cm is walking away from the base of a lamp-post at a speed of 1.2 m/sec. If the lamp-post is 3.6 m above the ground, find the length of her shadow after 4 seconds.

Answer:

Let the length of the shadow at a distance of 4.8 m from the lamp post = x cm.
From the figure,
△ABE ~ △DCE
[∵ ∠B = ∠C = 90°
∠E = ∠C common
(A.A. similarity)]
Hence,
AB/DC = BE/CE = AE/DE
∴ 360/90 = 480+x/x
⇒ 4 = 480+x/x
⇒ 4x = 480 + x
⇒ 4x - x = 480
⇒ 3x = 480
⇒ x = 160 cm = 1.6 m
∴ Length of the shadow = 1.6 m

Question 4.
CM and RN are respectively the medians of similar triangles △ABC and △PQR. Prove that

i) △AMC ~ △PNR
ii)CM/RN = AB/PQ
iii) △CMB ~ △RNQ

Answer:
Given : △ABC ~ △PQR
CM is a median through C of △ABC.
RN is a median through R of △PQR.
R.T.P:
i) △AMC ~ △PNR.
Proof: In △AMC and △PNR,

iii) △CMB ~ △RNQ
Proof: In △CMB and △RNQ
∠B = ∠Q [Corresponding angles of △ABC and △PQR]
Also, BC/RQ = BM/QN

Thus, △CMB ~ △RNQ by S.A.S similarity condition.

Question 5.
Diagonals AC and BD of a trapezium ABCD with AB ∥ DC intersect each other at the point ‘O’. Using the criterion of similarity for two triangles, show that OA/OC = OB/OD.

Answer:

Given : □ ABCD, AB ∥ DC
The diagonals AC and BD intersect at ‘O’.
R.T.P: OA/OC = OB/OD
Construction: Draw EF ∥ AB, passing through ‘O’.
Proof: In △ACD, OE ∥ CD [∵ Construction]
Hence OA/OC = EA/ED …….. (1)
(∵ Line drawn parallel to one side of a triangle divides other two sides in the same ratio - Basic proportionality theorem)
Also in △ABD, EO ∥ AB [Construction] Hence,
EA/ED = OB/OD ……… (2)
(∵ Basic proportionality theorem) From (1) and (2), we have
OA/OC = OB/OD
∴ Hence proved.

Question 6.
AB, CD, PQ are perpendicular to BD. AB = x, CD = y and PQ = z, prove that 1/x + 1/y = 1/z.

Answer:
Given ∠B = ∠Q = ∠D = 90°
Thus, AB ∥ PQ ∥ CD.
Now in △BQP, △BDC
∠B = ∠B (Common)
∠Q = ∠D (90°)
∠P = ∠C [∵ Angle Sum property of triangles]
∴ △BQP ~ △BDC
(by A.A.A similarity condition)
Hence BQ/BD = PQ/CD
[∵ Ratio of corresponding sides is equal] Also in △DQP and △DBA
∠D = ∠D (Common)
∠Q = ∠B (90°)
∴ △DQP ~ △DBA (by A.A. similarity condition)
QD/BD = PQ/AB
[ Ratio of corresponding sides is equal]
Adding (1) and (2), we get

Question 7.
A flag pole 4 m tall casts a 6 m., shadow. At the same time, a nearby building casts a shadow of 24 m. How tall is the building?

Answer:
Given: 4 m length flag pole casts a shadow 6 m.
Let x m length/tall building casts a shadow 24 m.

Let AB be the length of flag pole = 4 m.
Shadow of AB = BC = 6 m.
PQ be the building = x m (say)
QR, the shadow of the building = 24 m
From the figure,
∠A = ∠P
∠B = ∠Q
∴ △ABC ~ △PQR by A.A. similarity condition
Hence AB/PQ = BC/QR
[∵ Ratio of corresponding angles is equal]
4/6=x/24
x = 24×4/6= 16 m
∴ Height of the building = 16 m.

Question 8.
CD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of △ABC and △FEG respectively. If △ABC ~ △FEG then show that

i)CD/GH = AC/FG
ii) △DCB ~ △HGE
iii) △DCA ~ △HGF

Answer:

Given: △ABC ~ △FEG.
CD is the bisector of ∠C and GH is the bisector of ∠G.
R.T.P.:
i)CD/GH = AC/FG
In △ACD and △FGH
∠A = ∠F
[∵ Corresponding angles of △ABC and △FEG]
∠ACD = ∠FGH
[∵ ∠C = ∠G ⇒ 1/2 ∠C = 1/2 ∠G ⇒ ∠ACD = ∠FGH]
∴ By A.A. similarity condition, △ACD ~ △FGH
AC/FG = CD/GH = AD/FH
[∵ Ratio of the Corresponding angles is equal]
⇒ AC/FG = CD/GH [Q.E.D]

ii) △DCB ~ △HGE
In △DCB and △HGE,
∠B = ∠E
[∵ Corresponding angles of △ABC and △FEG]
∠DCB = ∠HGE
[∵ ∠C = ∠G ⇒ 1/2 ∠C =1/2 ∠G ⇒ ∠DCB = ∠HGE]
∴ △DCB ~ △HGE . (by A.A. similarity condition)

iii) △DCA ~ △HGF
In △DCA and △HGF
∠A = ∠F
12∠C = 1/2 ∠G ⇒ ∠DCA = ∠HGF
[∵ Corresponding angles of the similar triangles]
∴ △DCA ~ △HGF
[ A.A. similarity condition]

Question 9.
AX and DY are altitudes of two similar triangles △ABC and △DEF. Prove that AX : DY = AB : DE.

Answer:

Given: △ABC ~ △DEF.
AX ⊥ BC and DY ⊥ EF.
R.T.P.: AX : DY = AB : DE.
Proof: In △ABX and △DEY ∠B = ∠E [∵ Corresponding angles of △ABC and △DEF]
∠AXB = ∠DYE [given]
∴ △ABX ~ △DEY
(by A.A. similarity condition)
Hence AB/DE = BX/EY = AX/DY
[∵ Ratios of corresponding sides of similar triangles are equal]
⇒ AX : DY = AB : DE [Q.E.D.]

Question 10.
Construct a triangle shadow similar to the given ?ABC, with its sides equal to 5/3 of the corresponding sides of the triangle ABC.

Answer:

Question 11.
Construct a triangle of sides 4 cm, 5 cm and 6 cm. Then, construct a triangle similar to it,whose sides are 2/3 of the corresponding sides of the first triangle.

Answer:

Question 12.
Construct an isosceles triangle whose base is 8 cm and altitude is 4 cm. Then, draw another triangle whose sides are 1 1/2 times the corresponding sides of the isosceles triangle.

Answer:

Steps of construction:

Draw AABC in which BC = 8 cm and altitude AD = 4 cm.
Draw a ray BX making an acute angle with BC on the side opposite to vertex A.
Mark three points B₁, B₂and B₃such that BB₁= B₁B₂= B₂B₃.
Join B₂C.
Draw a line parallel to B₂C through B₃meeting BC produced C’.
Draw a line paral1e1 to AC through C’ meeting BA produced at A’.
△A’BC’ is the required triangle.

Question 1.
Equilateral triangles are drawn on the three sides of a right angled triangle. Show that the area of the triangle on the hypotenuse is equal to the sum of the areas of triangles on the other two sides.

Answer:

Let △PQR is a right angled triangle, ∠Q = 90°
Let PQ = a, QR b and
PR = hypotenuse = c
Then from Pythagoras theorem we can
say a²+ b²= c²……… (1)
△PSR is an equilateral triangle drawn on hypotenuse
∴ PR = PS = RS = c,
Then area of triangle on hypotenuse
√3/4 c²……… (2)
△QRU is an equilateral triangle drawn on the side ‘QR’ = b
∴ QR = RU = QU = b
Then area of equilateral triangle drawn on the side = √3/4 b²……… . (3)
△PQT is an equilateral triangle drawn on another side ‘PQ’ = a
∴ PQ = PT = QT = a
Area of an equilateral triangle drawn an another side ‘PQ’ = √3/4 a² ……….. (4)
Now sum of areas of equilateral triangles on the other two sides

= Area of equilateral triangle on the hypotenuse.
Hence Proved.

Question 2.
Prove that the area of the equilateral triangle described on the side of a square is half the area of the equilateral triangles described on its diagonal.

Answer:

triangle on the side of square.
Hence Proved.

Question 3.
D, E, F are midpoints of sides BC, CA, AB of △ABC. Find the ratio of areas of △DEF and △ABC.

Answer:

Given in △ABC D, E, F are the midpoints of the sides BC, CA and AB.
In △ABC, EF is the line join of mid-points of two sides AB and AC of △ABC.
Thus FE ‖ BC [∵ AF/FB = AE/EC Converse of B.P.T.]
Similarly DE divides AC and BC in the same ratio, i.e., DE ‖ AB.
Now in □ BDEF, both pairs of opposite sides (BD ‖ EF and DE ‖ BF) are parallel.
Hence □ BDEF is a parallelogram where DF is a diagonal.
∴ △BDF ≃ △DEF ……… (1)
Similarly we can prove that
△DEF ≃ △CDE ……… (2)
[∵ CDFE is a parallelogram]
Also, △DEF ≃ △AEF …….. (3)
[∵ □ AEDF is a parallelogram]
From (1), (2) and (3)
△AEF ≃ △DEF ≃ BDF ≃ △CDE
Also, △ABC = △AEF + △DEF + △BDF + △CDE = 4 . △DEF
Hence, △ABC : △DEF = 4 : 1.

Question 4.
In △ABC, XY ‖ AC and XY divides the triangle into two parts of equal area. Find the ratio of AX/XB.

Answer:

Given: In ∠ABC, XY ‖ AC.
XY divides ∠ABC into two points of equal area.
In ∠ABC, ∠XBY
∠B = ∠B
∠A = ∠X
∠C = ∠Y
[∵ XY ‖ AC; (∠A, ∠X) and ∠C, ∠Y are the pairs of corresponding angles]
Thus ∠ABC ~ ∠XBY by A.A.A similarity condition.
Hence △ABC/△XBY=AB²/XB²
[∵ The ratio of areas of two similar triangles is equal to the ratio of squares of their corresponding sides]

⇒ AX/XB + 1 = √2 ⇒ AX/XB = √2 - 1 Hence the ratio AX/XB = √2-1/1.

Question 5.
Prove that the ratio of areas of two similar triangles is equal to the square of the ratio of their corresponding medians.

Answer:

Given: △ABC ~ △XYZ
R.T.P: △ABC/△XYZ = AD^{2/XW^{2

Proof : We know that the ratio of areas of two similar triangles is equal to the ratio of the squares of their corresponding sides.}}

Hence the ratio of areas of two similar triangles is equal to the squares of ratio of their corresponding medians.

Question 6.
△ABC ~ △DEF. BC = 3 cm, EF = 4 cm and area of △ABC = 54 cm². Determine the area of △DEF.

Answer:

Given: △ABC ~ △DEF
BC = 3 cm
EF = 4 cm
△ABC = 54 cm²
∴ △ABC ~ △DEF, we have
△ABC/△DEF=BC²/EF²
[∵ The ratio of two similar triangles is equal to the ratio of the squares of the corresponding sides].
54/△DEF=3²/4²
∴ △DEF =54×16/9= 96 cm²

Question 7.
ABC is a triangle and PQ is a straight line meeting AB in P and AC in Q. If AP = 1 cm and BP = 3 cm, AQ =1.5 cm, CQ = 4.5 cm. Prove that area of △APQ = 1/16 (area of △ABC).

Answer:

[∵ Ratio of two similar triangles is equal to the ratio of the squares of their corresponding sides].
= 1²/(3+1)² = 1/16 [∵ AB = AP + BP = 1 + 3 = 4 cm]
∴ △APQ = 1/16 (area of △ABC) [Q.E.D]

Question 8.
The areas of two similar triangles are 81 cm²and 49 cm²respectively. If the altitude of the bigger triangle is 4.5 cm. Find the corresponding altitude of the smaller triangle.

Answer:
Given: △ABC ~ △DEF
△ABC = 81 cm²
△DEF = 49 cm²
AX = 4.5 cm
To find: DY
We know that,
△ABC/△DEF=AX²/DY²
[∵ Ratio of areas of two similar triangles is equal to ratio of the squares of their corresponding altitudes]

∴ DY = 3.5 cm.

Question 1.
Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals.

Answer:

Given : □ ABCD is a rhombus.
Let its diagonals AC and BD bisect each other at ‘O’.
We know that “the diagonals in a rhombus are perpendicular to each other”.
In △AOD; AD²= OA²+ OD²………. (1)
[Pythagoras theorem]
In △COD; CD²= OC²+ OD²………. (2)
[Pythagoras theorem]
In △AOB; AB²= OA²+ OB²………. (3)
[Pythagoras theorem]
In △BOC; BC²= OB²+ OC²………. (4)
[Pythagoras theorem]
Adding the above equations we get AD²+ CD²+ AB²+ BC²= 2 (OA²+ OB2 + OC²+ OD²)

Question 2.
ABC is a right triangle right angled at B. Let D and E be any points on AB and BC respectively. Prove that AE²+ CD²= AC²+ DE².

Answer:
Given: In △ABC; ∠B = 90°
D and E are points on AB and BC.
R.T.P.: AE²+ CD²= AC²+ DE²
Proof: In △BCD, △BCD is a right triangle right angled at B.
∴ BD²+ BC²= CD²……… (1)
[∵ Pythagoras theorem states that hypotenuse²= side²+ side²]
In △ABE; ∠B = 90°
Adding (1) and (2), we get
BD²+ BC²+ AB²+ BE² CD²+ AE²
(BD²+ BE²) + (AB²+ BC²) = CD²+ AE²
DE²+ AC² - CD²+ AE²[Q.E.D.]
[∵ (i) In △DBE, ∠B = 90° and DE²= BD²+ BE²
(ii) In △ABC, ∠B = 90° and AB²+ BC²]

Question 3.
Prove that three times the square of any side of an equilateral triangle is equal to four times the square of the altitude.

Answer:
Given: △ABC, an equilateral triangle;
AD - altitude and the side is a units, altitude h units.
R.T.P: 3a²= 4h²

Proof: In △ABD, △ACD
∠B = ∠C [∵ 60°]
∠ADB = ∠ADC [∵ 90°]
∴ ∠BAD = ∠DAC [∵ Angle sum property]
Also, BA = CA
∴ △ABD s △ACD (by SAS congruence condition)
Hence, BD = CD = 1/2 BC = a/2 [∵ c.p.c.t]
Now in △ABD, AB²= AD²+ BD²
[∵ Pythagoras theorem]
a²= h²+(a/2)²
a²= h²+a²/4
h²=4a²-a²/4
∴ h²=3a²/4
⇒ 4h²= 3a²(Q.E.D)

Question 4.
PQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR. Show that PM² = QM . MR.

Answer:

Given: In △PQR, ∠P = 90° and PM ⊥ QR.
R.T.P : PM² = QM . MR
Proof: In △PQR; △MPR
∠P = ∠M [each 90°]
∠R = ∠R [common]
∴ △PQR ~ △MPR ……… (1)
[A.A. similarity]
In △PQR and △MQP,
∠P = ∠M (each 90°)
∠Q = ∠Q (common)
∴ △PQR ~ △MQP ……… (2)
[A.A. similarity]
From (1) and (2),
△PQR ~ △MPR ~ △MQP [transitive property]
∴ △MPR ~ △MQP
MP/MQ = PR/QP = MR/MP
[Ratio of corresponding sides of similar triangles are equal]
PM/QM = MR/PM
PM . PM = MR . QM
PM² = QM . MR [Q.E.D]

Question 5.
ABD is a triangle right angled at A and AC ⊥ BD.
Show that (i) AB²= BC BD

(ii) AD²= BD CD
(iii) AC²= BC DC.

Answer:
Given: In △ABD; ∠A = 90° AC ⊥ BD
R.T.P.:
i) AB²= BC . BD
Proof: In △ABD and △CAB,
∠BAD = ∠ACB [each 90°]
∠B = ∠B [common]
∴ △ABD ~ △CBA
[by A.A. similarity condition]
Hence,AB/BC = BD/AB = AD/AC
[∵ Ratios of corresponding sides of similar triangles are equal]
AB/BD=BC/AB
⇒ AB . AB = BC . BD
∴ AB²= BC . BD

ii) AD²= BD . CD
Proof: In △ABD and △CAD
∠BAD = ∠ACD [each 90°]
∠D = ∠D (common)
∴ △ABD ~ △CAD [A.A similarity]
Hence,AB/AC = BD/AD = AD/CD
⇒ BD/AD = AD/CD
AD . AD = BD . CD
AD²= BD . CD [Q.E.D]

iii) AC²= BC . DC
Proof: From (i) and (ii)
△ACB ~ △DCA
[∵ △BAD ~ △BCA ~ △ACD
Hence,AC/DC = BC/AC = AB/AD
AC/DC=BC/AC
AC . AC = BC . DC
AC²= BC . DC [Q.E.D]

Question 6.
ABC is an isosceles triangle right angled at C. Prove that AB²= 2AC².

Answer:

Given: In △ABC; ∠C = 90°; AC = BC.
R.T.P.: AB²= 2AC²
Proof: In △ACB; ∠C = 90°
Hence, AC²+ BC²= AB²
[Square of the hypotenuse is equal to sum of the squares of the other two sides - Pythagoras theorem]
⇒ AC²+ AC² = AB²[∵ AC = BC given]
⇒ AB²= 2AC² [Q.E.D.]

Question 7.
‘O’ is any point in the interior of a triangle ABC.
OD ⊥ BC, OE ⊥ AC and OF ⊥ AB, show that

i) OA²+ OB²+ OC²- OD²- OE²- OF²= AF²+ BD²+ CE²
ii) AF²+ BD²+ CE²= AE²+ CD²+ BF².

Answer:
Given: △ABC; O’ is an interior point of △ABC.
OD ⊥ BC, OE ⊥ AC, OF ⊥ AB.
R.T.P.:
i) OA²+ OB²+ OC²- OD²- OE²- OF²= AF²+ BD²+ CE²
Proof: In OAF, OA²= AF²+ OF²[Pythagoras theorem]
⇒ OA²- OF²= AF²…….. (1)
In △OBD,
OB²= BD²+ OD²
⇒ OB²- OD²= BD²…….. (2)
In △OCE, OC²= CE²+ OE²
OC²- OE²= CE²……… (3)
Adding (1), (2) and (3) we get,
OA²- OF²+ OB²- OD²+ OC²- OE²= AF²+ BD²+ CE²
OA²+ OB²+ OC²- OD²- OE²- OF²= AF²+ BD²+ CE²……… (4)

ii) AF²+ BD²+ CE²= AE²+ CD²+ BF²
In △OAE,
OA²= AE²+ OF²……… (1)
⇒ OA²- OE²= AE²
In △OBF, OB²= BF²+ OF²
OB²- OF²= BF²……… (2)
In △OCD, OC²= OD²+ CD²
OC²- OD²= CD²……… (3)
Adding (1), (2) and (3) we get
OA²- OE²+ OB²- OF²+ OC²- OD²= AE²+ BF²+ CD²
⇒ OA²+ OB²+ OC²- OD²- OE²- OF²= AE²+ CD²+ BF²
⇒ AF²+ BD²+ CE²= AE²+ CD²+ BF²[From problem (i)]

Question 8.
A wire attached to vertical pole of height 18 m is 24 m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?

Answer:

Height of the pole AB = 18 m.
Length of the wire AC = 24 m.
Distance beween the pole and the stake be ‘d’ meters.
By Pythagoras theorem,
Hypotenuse²= side²+ side²
24²= 18²+ d²
d²= 24²- 18²= 576 - 324 = 252
= √36×7
∴ d = 6√7 m.

Question 9.
Two poles of heights 6 m and 11m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.

Answer:

Let the height of the first pole AB = 6 m.
Let the height of the second pole CD = 11 m.
Distance between the poles AC = 12 m.
From the figure □ ACEB is a rectangle.
∴ AB = CE = 6 m
ED = CD - CE = 11 - 6 = 5 m
Now in △BED; ∠E = 90°; DE = 5 m; BE = 12 m
BD²= BE²+ DE²
[hypotenuse²= side²+ side² - Pythagoras theorem]
= 12²+ 5²
= 144 + 25
BD²= 169
BD = √l69 = 13m
∴ Distance between the tops of the poles = 13 m.

Question 10.
In an equilateral triangle ABC, D is a point on side BC such that BD = 1/3 BC. Prove that 9AD² = 7AB².

Answer:

⇒ 28 AB²= 36 AD²
⇒ 7 AB²= 9 AD²
Hence proved.

Question 11.
In the given figure, ABC is a triangle right angled at B. D and E are points on BC trisect it. Prove that 8 AE²= 3 AC²+ 5 AD².

Answer:
In △ABC, ∠B=90°

∴ RHS of (3) and (4) are equal.
∴ LHS of (3) and (4) are equal.
∴ 8 AE² = 3 AC² + 5 AD².
Hence proved.

Question 12.
ABC is an isosceles triangle right angled at B. Equilateral triangles ACD and ABE are constructed on sides AC and AB. Find the ratio between the areas of △ABE and △ACD.

Answer:

Given: △ABC, AB = BC and ∠B = 90°
△ABE on AB; △ACD on AC are equiangular triangles.
Let equal sides of the isosceles right triangle, AB = BC = a (say)
Then, in △ABC, ∠B = 90°
AC²- AB²+ BC²
[hypotenuse² = side²+ side²- Pythagoras theorem] = a²+ a²= 2a²
Since, △ABE ~ △ACD
△ABE/△ACD=AB²/AC²
[∵ Ratio of areas of two similar tri-angles is equal to the ratio of squares of their corresponding sides]
=a²/2a²= 1/2
△ABE : △ACD = 1 : 2.

Important Question

6th Lesson Triangles Class 10 Important Questions with Solutions

10th Class Maths Triangles 1 Mark Important Questions

Question 1.
Write the properties of similar triangles.

Answer:
Two triangles are said to be similar, if their

corresponding angles are equal.
corresponding sides are proportional.

Question 2.
Write the examples of similar figures.

Answer:
All circles, all squares, all equilateral triangles, etc.

Question 3.
State the Thales theorem.

Answer:
If a line drawn parallel to one side of a triangle intersecting the other two sides, then it divides the two sides in the same ratio.

Question 4.
State the converse of basic proportionality theorem.

Answer:
If a line divides any two sides of a tri¬angle in the same ratio, then the line must be parallel to the third side.

Question 5.
State the pythagoras theorem.

Answer:
In a right angled triangle square of the hypotenuse is equal to the sum of the squares of the other two sides.
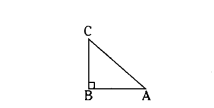That is in ΔABC, ∠B = 90° then AC² = AB² + BC².

Question 6.
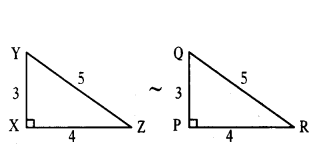
In ΔABC and ΔDEF, AB/DE = BC/FD. Which of the following makes the two triangles similar ?

A) ∠A = ∠D
B) ∠B = ∠D
C) ∠B = ∠E
D) ∠A = ∠F

Solution:
B) ∠B = ∠D

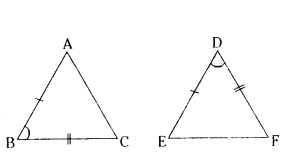
AB/DE = BC/FD
∴ ∠B = ∠D
ΔABC ~ ΔEDF

Question 7.
In the given fig. DE ‖ BC. Find BC.

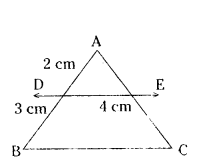
Solution:
AD/AB = DE/BC
2/2+3 = 4/BC
2/5 = 4/BC
2BC = 20
BC = 10 cm.

Question 8.
In ΔABC, PQ ‖ BC. If PB = 6 cm, AP = 4 cm, AQ = 8 cm, find the length of AC.

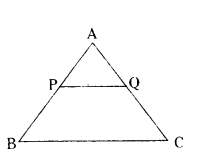
Solution:
PQ ‖ BC
By BPT

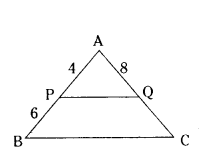
4/6 = 8/QC
2/3 = 8/QC
2QC = 24
QC = 12
AC = 8 + 12 = 20 cm

Question 9.

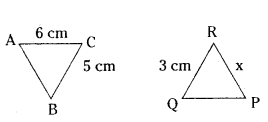
In the given figure, ΔABC ~ ΔQPR, If AC = 6 cm, BC = 5 cm, QR = 3 cm and PR = x; then the value of x is :

Solution:
ΔABC ~ ΔQPR

6/3 = 5/2
2 = 5/x
x = 5/x = 2.5 cm

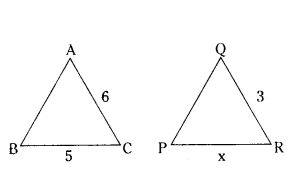
Question 10.
If in ΔABC and ΔPQR, AB/QR = BC/PR = CA/PQ then :
A) ΔPQR ~ ΔCAB
B) ΔPQR ~ ΔABC
A) ΔCBA ~ ΔPQR
B) ΔBCA ~ ΔPQR

Solution:
A) ΔPQR ~ ΔCAB
ΔPQR ~ ΔCAB

Question 11.
Which of the following is not a similarity criterion of triangle ?
A) AA
B) SAS
C) AAA
D) RHS

Answer:
D) RHS

Question 12.
If ΔABC, AB = 6√3 cm, AC = 12 cm and BC = 6 cm, then ∠B = ..... .

Solution:

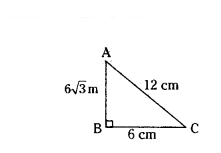
AB² = (6√3)² = 36 × 3 = 108
AC² = 12² - 144
BC² = 6² = 36
AC² = AB² + BC²
144 = 108 + 36
144 = 144
∠B = 90°

Question 13.
In the given fig. DE ‖ BC. Which of the following is true ?

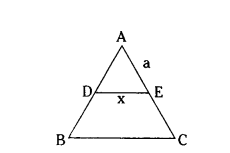
A) x = a+b/ay
B) y = ax/a+b
C) x = ay/a+b
D) x/y = a/b
Solution:
C) x = ay/a+b
DE ‖ BC, ΔADE ~ ΔABC
a/x = a+b/y
x(a + b) = ay
x = ay/a+b

Question 14.
In ΔABC and ΔDEF, ∠F = ∠C, ∠B = ∠E and AB = 1/2 DE then the two triangles are

A) congruent, but not similar not congruent
B) similar, but not congruent
C) neither congruent nor similar
D) congruent as well as similar

Solution:
B) similar, but not congruent

AB = 1/2 DE
2AB = DE
ΔABC ~ ΔDEF but not congruent.

Question 15.
In the given fig. If DE ‖ BC. Find EC.

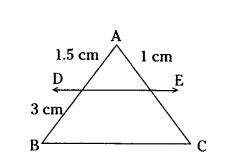
DE ‖ BC
AD/DB = AE/EC
1.5/3 = 1/EC
EC = 2 cm

Question 16.
In the given figure, AD = 2 cm, DB = 3 cm, DE = 2.5 cm and DE ‖ BC. Find the value of x.

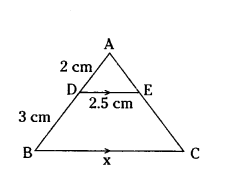
Solution:
ΔADE ~ ΔABC
AD/DB = DE/x
2/5 = 2.5/x
2x = 2.5 × 5
x = 2.5 × 5/2
x = 2.5 × 2.5
x = 6.25 cm

Question 17.
In two triangles ΔPQR and ΔABC, it is given that AB/BC = PQ/PR For these two triangles to be similar, which of the following should be true ?

A) ∠A = ∠P
B) ∠B = ∠Q
C) ∠B = ∠P
D) ∠A = ∠R

Solution:
C) ∠B = ∠P

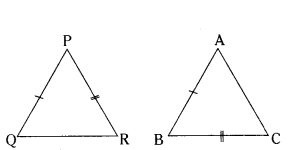
AB/BC = PQ/PR
AB/PQ = BC/PR
ΔPQR ~ ΔBAC
∠P = ∠B.

Question 18.
In ΔABC, DE ‖ BC, AD = 4 cm, BD = 6 cm and AE = 5 cm, find the length of EC.

Solution:

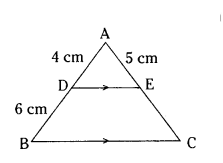
DE ‖ BC
By BPT
4/6 = 5/EC
2/3 = 5/EC
EC = 15/2 = 7.5 cm

Question 19.
In ΔABC, DE ‖ BC, AD = 2 cm, BD = 3 cm, DE: BC is equal to ...... .

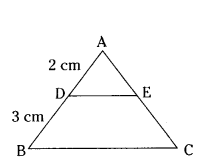
Solution:
DE ‖ BC, ΔADE, ΔBC
∠ A = ∠A (Common angle)
∠D = ∠B (Corresponding angle) by AA Similarity
ΔADE ~ ΔABC
AD/AB = AE/AC = DE/BC
2/2+3 = DE/BC
2/5 = DE/BC
DE : BC = 2 : 5

Question 20.
In the given fig. DE ‖ BC. If AD = 3 cm, AB = 7 cm and EC = 3 cm, then find the length of AE.

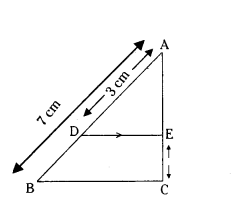
DE ‖ BC, BD = 7 - 3 = 4 cm
By BPT 3/4 = AE/3
4AE = 9
AE = 9/4
AE = 2.25 cm.

Question 21.
The perimeters of two similar triangles are 24 cm and 18 cm respectively. If one side of the first triangle is 8 cm then what is the corresponding side of second triangle ?

Answer:
6

Question 22.
In ΔABC, ∠B = 90°, BD ⊥ AC.
If AD = 8 cm and BD = 4 cm, then what is the length of CD ?

Answer:
2 cm.

Question 23.
Among "Circles", "Squares" and "Triangles", which are always similar ?

Answer:
Circles and squares are always similar.

Question 24.
In ΔABC and ΔDEF,
if ∠B = ∠E, ∠C = ∠F, then which of the following is a true statement ?

A) AB/DE = CA/EF
B) BC/EF = AB/FD
C) AB/DE = BC/EF
D) CA/FD = AB/EF
Answer:
C) AB/DE = BC/EF

Question 25.
Given DE ‖ BC, AD = 4.5 cm, BD = 9 cm, and EC = 8 cm. What is the length of AE?

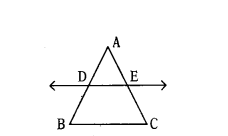
Solution:
AD = 4.5 cm, BD = 9 cm, EC = 8 cm
AD/DB = AE/EC ⇒ 4.5/9 = AE/8 ⇒ 9AE = 36
∴ AE = 4 cm

Question 26.
The sides of two equilateral triangles ABC and DEF are 4 cm. and 5 cm. respeclively. Find ar(△DEF)/ar(△ABC).

Solution:
Ratio of areas of Δ = (Ratio of corresponding sides)²
ar(△DEF)/ar(△ABC) = 5²/4² = 1/2

Question 27.
ΔABC ~ ΔDEF and ∠A = ∠D = 90°, find the measure of ∠B + ∠F.

Solution:
ΔABC ~ ΔDEF
⇒ ∠A = ∠D = 90°
∠B = ∠E; ∠C = ∠F
Now in ΔABC, ∠A + ∠B + ∠C = 180°
Now putting ∠A = ∠D = 90°
⇒ 90° + ∠B + ∠C = 180°
⇒ ∠B + ∠C = 90°
Now putting ∠C = ∠F
⇒ ∠B + ∠F = 90°

Question 28.
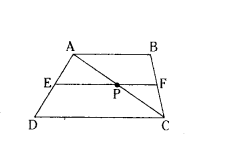
Given AB ‖ CD, identify the pair of similar triangles in this image and justify.

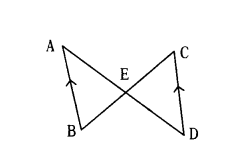
Solution:
∠AEB = ∠CED (Vertically opp. angle)
∴ ∠BEA and ∠CDE are similar by AAA - Similarity rule
ΔBEA ~ ΔCDE

Question 29.
ABC is a triangle in which

p) If AB² + BC² = AC² then
q) BC² + AC² = AB² then
r) CA² + AB² = BC² then

i) ∠A = 90°
ii) ∠B = 90°
iii) ∠C = 90°

A) p - i, q - ii, r - iii
B) p - ii, q - i, r - iii
C) p - iii, q - i, r - ii
D) p - ii, q - iii, r - i

Answer:
D) p - ii, q - iii, r - i

Question 30.
Statement-I: The lengths 3 cm, 4 cm, 5 cm form a right angled triangle. Statement-II: If ‘a’ is the side of an equilateral triangle, then its height is √3 a. Now, choose the correct answer.

(A) Statement-I and Statement-II both are True.
(B) Statement-I and Statement-II both are False.
(C) Statement-I is True. Statement-II is False.
(D) Statement-I is False. Statement-II is True.
Answer:
C) Statement-I is True. Statement-II is False.

Question 31.
Give two different examples of pair of similar figures.

Answer:
(i) Two equilateral triangles.
(ii) Two circles.

Question 32.
"In a right triangle, the square of hypotenuse is equal to the sum of the squares of the other two sides." The above theorem is related to which Mathematician ?

A) Baudhayan
B) Aryabhatta
C) Euclid
D) Bhaskaracfyarya
Answer:
A) Baudhayan

Question 33.
Assertion (A) : The sides of two similar triangles are in the ratio 2 : 5, then the areas of these triangles are in the ratio 4 : 25
Reason (R) : The ratio of the areas of two similar triangles is equal to the square of the ratio of their sides.

A) Both assertion and reason are true and reason is the correct explanation of assertion.
B) Both assertion and reason are true but reason is not the correct explanation of assertion.
C) Assertion is true but reason is false.
D) Assertion is false but reason is true.
Answer:
A) Both assertion and reason are true and reason is the correct explanation of assertion.

10th Class Maths Triangles 2 Marks Important Questions

Question 1.
In the figure, if RS // ID then find AR.

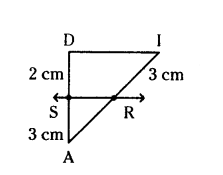
Given,
In ΔADI, RS // ID
By Thales theorem,
AS/DS = AR/IR
3/2 = AR/3
AR = 3×3/2 = 9/2 = 4.5 cm
Therefore AR = 4.5 cm.

Question 2.
In ΔABC, D and E are point on the sides of AB and AC respectively. Such that DE // BC. If AD/DB = 2/3 and AC = 18 cm, find AE.

Solution:

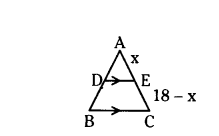
Given in ΔABC, DE // BC, AD/DB = 2/3,
AC = 18 cm
Let AE = x then EC = 18 - x.
In ΔABC, DE // BC
By Thales theorem
AD/DB = AE/EC
2/3 = x/18-x
3x = 2(18 - x)
3x = 36 - 2x
3x + 2x = 36
5x = 36
x = 36/5 = 7.2 cm
Therefore, AE = 7.2 cm.

Question 3.
In the figure, if AB ⊥ BC and DE ⊥ AC. Prove that ΔABC ~ ΔAED.

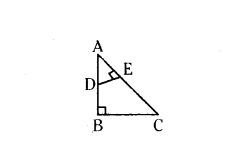
Solution:
Given in ΔABC, ∠B = 90°, ∠E = 90°
that is AB ⊥ BC and DE ⊥ AC.
In ΔABC, ΔAED
∠ABC = ∠AED = 90° (Angle)
∠BAC = ∠DAE (Common angle)
Therefore by Angle-Angle criterian of similarity
ΔABC ~ ΔAED

Question 4.
A vertical stick 10 cm long casts a shadow 8 cm long. At the same time a tower casts a shadow 30 m long. Determine the height of the tower.

Solution:
Given length of stick AB =10 cm
length of its shadow BC = 8 cm
Height of tower PQ = x cm.

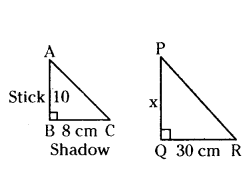
length of the shadow of tower at the same time QR = 30 cm.
By Angle-Angle similarity
ΔABC ~ ΔPQR
then the corresponding sides are in proportion.
AB/PQ = BC/QR
10/x = 8/30
8x = 30 × 10
x = 30×10/8 = 75/2 = 37.5 cm
Therefore, height of tower = 37.5 cm.

Question 5.
A vertical stick of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts the shadow 28 m long. Find the height of the tower.

Solution:

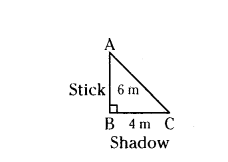
Let length of stick AD = 6 m
Length of its shadow DI = 4 m
Let height of tower SR = x m
and its shadow at the same time BE = 28 m.
By Angle-Angle similarity
ΔADI ~ ΔSRE
then the corresponding sides are in proportion

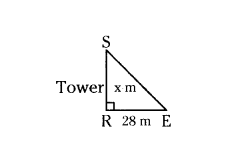
AD/SR = DI/RE
6/4 = x/28
x = 6/4 × 28 = 42 m
Therefore, height of tower = 42 m.

Question 6.
The perimeter of two similar triangles ABC and PQR are respectively 36 cm and 24 cm. If PQ = 10 cm find AB.

Solution:
Given ΔABC ~ ΔPQR
So, ratio of the corresponding sides = ratio of their perimeters.

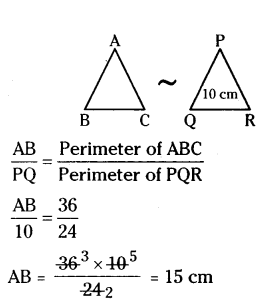
Therefore, AB = 15 cm

Question 7.
Is a square similar to a rectangle? Justify your answer.

Solution:
In a square and rectangle, the corresponding angles are equal. But the corresponding sides are not proportional.

∴ A square and a rectangle are not similar.

Question 8.
In ΔABC, LM//BC and AL/LB = 2/3, AM = 5 cm, find AC.

Solution:
In ΔABC, LM//BC
⇒ AL/LB = AM/MC (By B.P.T)

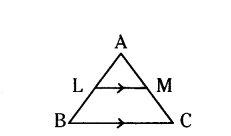
But = AL/LB = 2/3, so AM/MC = 2/3
Given AM = 5 cm and AM : MC = 2 : 3
AM/MC = 2/3 ⇒ 5/MC = 2/3
⇒ MC = 5×3/2 = 15/2 = 7.5
∴ AC = AM + MC = 5 + 7.5 = 12.5 cm

Question 9.

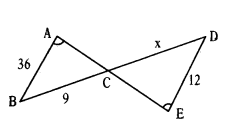
In the figure, ∠BAC = ∠CED, then verify whether the value of ‘x’ is 3 or not.

Solution:
Given : In ΔABC and ΔECD
∠A = ∠E
∠ACB = ∠ECD [∵ Vertically opposite]
∴ ∠B = ∠D [∵ Angle sum property]
∴ ΔABC - ΔEDC
⇒ AB/ED = BC/DC = AC/EC
⇒ 36/12 = 9/x
⇒ 36x = 108
⇒ x = 108/36 = 3

Question 10.
In ΔABC, DE ‖ BC and AC = 5.6 cm, AE = 2.1 cm, then find AD : DB.

Solution:

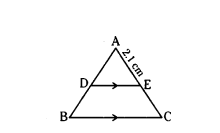
In ΔABC DE ‖ BC,
AE = 2.1 cm
EC = AC - AE = 5.6 - 2.1 = 3.5 cm
As per B.P.T, AD : DB = AE : EC = 2.1 : 3.5 = 3 : 5

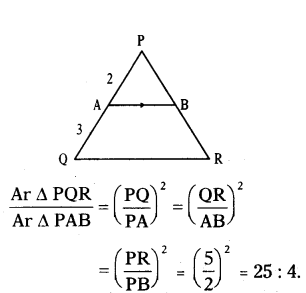
Question 11.
In the given figure, AB ‖ QR and PA = 2 cm, AQ = 3 cm, then find the ratio of areas of ΔPQR and ΔPAB.

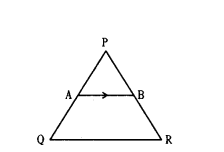
Solution:
Given AB ‖ QR; PA = 2, AQ = 3
then, ΔPQR ~ ΔPAB
∴ PQ = 2 + 3 = 5
∴ Ratio of area of similar triangles is equal to square of ratio of their corresponding sides.

Question 12.
In ΔPQR and ΔXYZ, it is given that ΔPQR ~ ΔXYZ, ∠Y + ∠Z = 90° and XY : XZ = 3 : 4. Then find the ratio of sides in ΔPQR.

Solution:
Given that ΔPQR - ΔXYZ means ∠P = ∠X, ∠Q = ∠Y and ∠R = ∠Z (∵ Corresponding angles are equal)
Similarly PQ/XY = QR/YZ = RP/ZX (∵ Ratio of corresponding sides)
Given that ∠Y + ∠Z = 90°

In AXYZ, ∠X + ∠Y + ∠Z = 180°
∠X + 90° = 180°
∠X = 180° - 90° = 90°
∠X + ∠P = 90° and XY/XZ
∴ ΔXYZ is a right angle triangle.
In a right angle triangle order of sides ratio may be 3 : 4 : 5.
* Remaining length YZ may be 5 units.
Ratio of XY : XZ : YZ = 3 : 4 : 5.
Similarly ratio of sides in ΔPQR is 3 : 4 : 5.

Question 13.
Find the value of ‘x’ in the given figure where ΔABC ~ ΔADE.

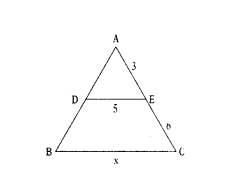
Solution:
ΔABC ~ ΔADE
⇒ AB/AD = BC/XE = AC/AE;
BC = x, DE = 5, AE = 3, AC = 9
By substituting BC/DE = AC/AE
∴ x/5 = 9/3 ⇒ x = 9×5/3 = 15
∴ x = 15 cm

Question 14.
It is given that ΔABC ~ ΔDEF. Is it true
to say that BC/DE = AB/EF ? Justify your answer.

Solution:
Given that ΔABC ~ ΔDEF
∴ AB/DE = BC/EF = AC/DF
(∵ Ratio of corresponding sides of similar triangles are equal)
But BE/DE = AB/EF (given)
∴ Given statement is wrong.

Question 15.
Srivani walks 12 m due East and turns left and walks another 5 m, how far is she from the place she started ?

Solution:
The distance of Srivani from the place she started

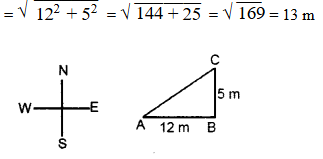
Question 16.
Write the similarity criterion by which the given pair of triangles are similar.

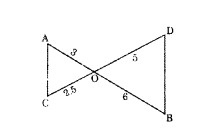
Solution:
OA/OB = 3/6 = 1/2
OC/OD = 2.5/5 = 0.5 = 1/2
OA/OB = OC/OD ⇒∠AOC = ∠BOD
Using SAS - Criterion ∴ ΔOAC ~ ΔOBD)

Question 17.
Madhavi said "All squares are simUar". Do you agree yith her statement ? Justify your answer.

Answer:
Because two polygons with the same number of sides are similar if
i) All the corresponding angles are equal and
ii) All the lengths of the corresponding sides are in the same ratio (or in proportion)
Squares size may not be equal but their ratios of corresponding parts will always be equal.

Question 18.
In the given figure, ABC is a triangle. AD = 3 cm, DB = 5 cm, AE = 6 cm and EC - 10 cm. Is DE ‖ BC ? Justify.

Solution:

AD = 3 cm, DB = 5 cm
AE = 6 cm, as EC = 10 cm
AD/DB = 3/5
AE/EC = 6/10 = 3/5
AD/DB = AE/EC ⇒ DE ‖ BC

Question 19.
The sides of a triangle measure 2√2, 4 and 2√6 units. Is it a right-angled triangle ? Justify.

Solution:
(2√2)² = 8
(4)² = 16
(2√6)² = 24
(2√2)² + (4)² - (2√6)²
∴ If sum of squares of two sides of a triangle is equal to the square of the third side, then the triangle is a right angled triangle. (Converse of Pythagorus theorem)
∴ Given triangle is a right-angled triangle.

Question 20.
In the given figure, if ABCD is a trapezium in which AB ‖ CD ‖ EF, then
AE BF prove that AE/ED = BF/FC.

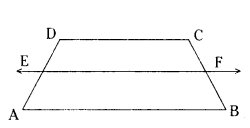
Solution:

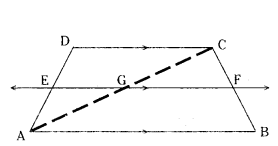
Given : In a trapezium ABCD, AB ‖ DC ‖ EF.
Given: AE/ED = BF/FC
Construction: Join AC which intersects EF at G.
Proof: ΔCAB, GF ‖ AB
FG/BF = CG/AG (by BPT)
BF/FC = AG/CG ..... (1)
In ΔADC, EG ‖ DC
AE/ED = AG/GC (by BPT) .. (2)
BY (1) & (2) AE/ED = BF/FC.

Question 21.
In figure, if AD = 6 cm, DB = 9 cm, AE - 8 cm and EC = 12 cm and ∠ADE=48°, Find ∠ABC.

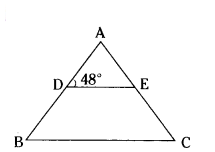
Solution:
In the figure AD = 6 cm
DB = 9cm
AE = 8 cm
EC = 12 cm
∠ADC = 48°
In ΔADE and ΔABC
AD/AB = 6/6+9 = 6/15 = 2/15
AE/AC = 8/8+12 = 8/20 = 2/5
∠A = ∠A (Common angle)
∴ by SAS criterion
ΔADE ~ ΔABC.
∠ADE = ∠ABC (by CPCT)
∴ ∠ABC = 48°

Question 22.
In the figure, altitudes AD and CE of ΔABC intersect each other at the point.
Show that
(i) ΔABD ~ ΔCBE
(ii) ΔPDC ~ ΔBEC

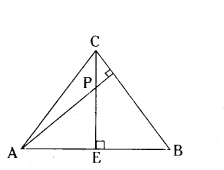
Solution:
i) Given ΔABD and ΔCBE
∠ADB = ∠CEB = 90°
∠B = ∠B (Common angle)
∴ By AA Similarity criterion
ΔADB ~ ΔCBE

ii) In ΔPDC and ΔBEC
∠PDC = ∠BEC = 90°
∠C = ∠C (Common angle)
∴ By AA similarity criterion
ΔPDC ~ ΔBEC.

10th Class Maths Triangles 4 Marks Important Questions

Question 1.
In ΔABC, P and Q are points on sides AB and AC respectively, such that PQ // BC. If AP = 2.4 cm, AQ = 2 cm, AC = 3 cm and BC = 6 cm. Find AB and PQ.

Solution:
Given in ΔABC, PQ // BC and AP = 2.4 cm, AQ = 2 cm, AC = 3 cm and BC = 6 cm
Let BP = x and PQ = y cm
By Thales theorem
AP/BP = AQ/CQ

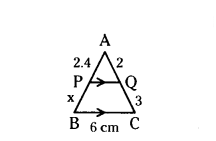
2.4/x = 2/3 and AP/AB = PQ/BC
2.4/x = 2/3 ⇒ 2x = 2.4 × 3 ⇒ x = 2.4×3/2
BP = x = 3.6 cm
∴ AB = AP + BP = 2.4 + 3.6 = 6 cm
Now, AP/AB = PQ/BC
2.4/6 = PQ/6
Therefore, PQ = 2.4 cm

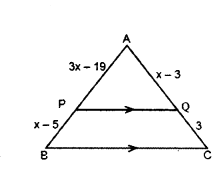
Question 2.
In the given trapezium ABCD, AB // DC. Find the value of x.

Solution:
In the given figure,
ABCD is a trapezium AB // DC.
OA = 3x - 19, OB = x - 3, OC = x - 5 and DO = 3 cm

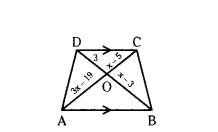
We know that diagonals of a trapezium divide each other proportionally,
AO/CO = BO/DO
3x-19/x-5 = x-3/3
3(3x - 19) = (x - 3) (x - 5)
9x - 19 × 3 = x² - 5x - 3x + 15
9x - x² + 8x - 57 - 15 = 0
- x² + 17x - 72 = 0
x² - 17x + 72 = 0
x² - 9x - 8x + 72 = 0
x(x - 9) - 8(x - 9) = 0
(x - 8) (x - 9) = 0
x - 8 = 0 (or) x - 9 = 0
Therefore, x = 8 (dr) x = 9

Question 3.
In the figure gIven AO/OC = BO/OD = 1/2 and AB = 5cm. Find the value of DC.

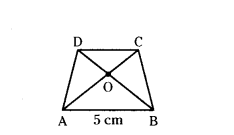
Solution:
In quadrilateral ABCD, diagonals AC and BD are meeting at O.
AO/OC = BO/OD = 1/2 and AB = 5cm.
In ΔAOB and ΔCOD
AO/OC = BO/OD and ∠AOB = ∠COD
by Side-Angle-Side similarity criterion
ΔAOB ~ ΔCOD
OA/OB = OB/OC = AB/DC
1/2 = 5/DC
DC = 2 × 5 = 10 cm
Therefore DC = 10 cm

Question 4.
In the given figure, OA/OC = OD/OB prove that ∠A = ∠C and ∠B = ∠D.

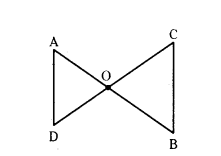
Solution:
Given in ΔAOD and ΔCOB
OA/OC = OD/OB
and ∠AOD = ∠BOC (Vertically opposite angles)
by Side-Angle-Side similarity criterion ΔAOD ~ ΔCOB
If two triangles are similar then their corresponding angles are equal,
i.e., ∠A = ∠C and ∠D = ∠B
Therefore, ∠A = ∠C and ∠B = ∠D.

Question 5.
A girl of height 90 cm is walking away from the base of a lamppost at a speed of 1.2 m/sec. If the lamp is 3.6 m above the ground, find the length of her shadow after 4 seconds.

Solution:

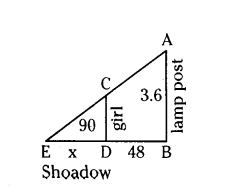
Let AB be the, height of lamp post
AB = 3.6 cm
and height of girl CD = 90 cm = 0.9 m length of the shadow of girl after 4 seconds = x m
length of BD = 1.2 × 4 = 4.8 cm
In ΔABE, ΔCDE
∠B = ∠D = 90° (Angle)
∠E = ∠E (Common angle)
By Angle-Angle similarity criterion
ΔABE ~ ΔCDE
then corresponding sides are in proportion.

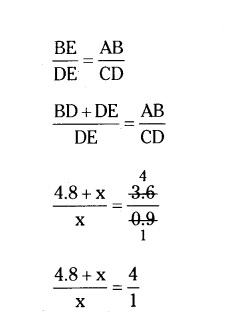
4x = 4.8 + x
4x - x = 4.8
3x = 4.8
x = 4.8/3 = 1.6 cm
Therefore length of shadow of the girls = 1.6 cm.

Question 6.
In the given figure, CD is the perpendicular bisector of AB. EF is perpendicular to CD. AE intersects CD
at G.Prove that CF/CD = FG/DG.

Solution:
In ΔEFC and ΔBDC
∠EFC = ∠BDC = 90°
∠ECF = ∠BCD (Common angle)
by AA Similarity
ΔEFC ~ ΔBDC
by CPST EF/BD = FC/DC.
In ΔEFG and ΔDGA
∠EGF = ∠DGA (VOA)
∠EFG = ∠GDA (= 90°)
by AA Similarity
Δ EFG ~ Δ ADG
we have AD = BD
EF/BD = FG/DG.
FG/DG = CF/CD.

Question 7.
In the given figure, ABCD is a parallelogram. BE bisects CD at M and intersects AC at L. Prove that EL = 2BL.

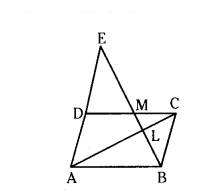
Solution:
Given ΔBMC and ΔEMD
∠BMC = ∠EMD (VOA)
Given MC = DM
∠BCM = ∠EDM (ALA)
∴ ΔBMC ≅ ΔEMD (by ASA)
by CPCT BC = DE
AE = AD + DE = BC + BC = 2BC
∴ ΔBLC ≅ ΔELA (by AA similarity)
EL/BL = AE/BC by CP/ST = EL/BL = 2BC/BC EL/BL = 2/1
EL = 2BL

Question 8.
In fig 6, if ΔABC ~ ADEF and their sides of lengths (in cm) are marked along them, then find the lengths of sides of each triangles.

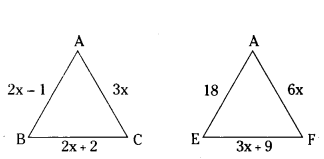
Solution:
ΔABC ~ ΔDEF.

4x - 2 = 18
4x = 20
x = 5
AB = 2 × 5 - 1 = 9.
BC = 2 × 5 + 2 = 12
CA = 3 × 5 = 15
DE = 18
EF = 3 × 5 + 9 = 24.
FD = 6 × 5 = 30
AB = 9 cm, BC = 12 cm, EF = 24 cm
CA = 15 cm, DE = 18 cm, FD = 30 cm.

Question 9.
The diagonals of a quadrilateral ABCD intersect each other at the point O such that AO/BO = CO/OD.

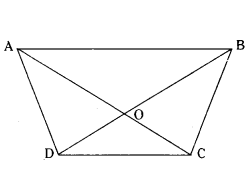
Show that quadrilateral ΔABCD is a trapezium.

Solution:
Given: The diagonals of a quadrilateral ΔBCD intersect each other at the point ‘O’ such that
AO/BO = CO/OD
To prove : ABCD is a trapezium.
Construction: Draw OE ‖ DC such that E lies on BC.

Proof : In ΔBDC
By BPT, BO/OD = BE/EC ... (1)
but AO/CO = BO/DO .... (2)
from (1) & (2)
AO/CO = BE/EC
by the converse of BPT.
OE ‖ AB
Since AB ‖ CE ‖ DC
∴ AB ‖ DC
∴ ΔBCD is a trapezium.

Question 10.
E is a point on the side AD produced of a parallelogram ABCD and BE interesects CD at F. Show that ΔABE ~ ΔCFB.

Solution:

In ΔABE and ΔCFB
∠ABE = ∠CFB (AIA)
∠BAE = ∠BCF (opposite angles of ‖gm)
∴ by AA Similarity criterion
ΔABE ~ ΔCFB.

Question 11.

In the given figure, CM and RN are respectively the medians of ΔABC and ΔPQR. If ΔABC ~ ΔPQR, then prove that ΔAMC ~ ΔPNR.

Solution:
Given : ΔABC ~ ΔPQR
CM and RN are medians of ΔABC and ΔPQR respectively.
To prove : ΔAMC ~ ΔPNR
Proof : Given ΔABC ~ ΔPQR, ∠A = ∠P,
∠B = Q, ∠C = ∠R
AB/PQ = BC/QR = CA/RP
AB/PQ = x+y/y+y = 2x/2y = x/y
Let AM = MB = x
In ΔAMC and ΔPNR
x/y = AM/PN
x/y = AB/PQ = CA/RP
AM/PN = CA/RP
∠A = ∠P
by SAS similarity criterion.
ΔABC ~ ΔPNR.

Question 12.
In figure ∠1 = ∠2 and ΔNSQ ≅ ΔMTR, then prove that ΔPTS ~ ΔPRQ.

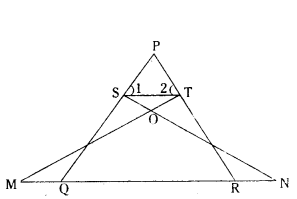
Solution:
Given ∠1 = ∠2
ΔNSQ ≅ ΔMTR
∴ PS = PT
by CPCT, SQ = TR
In ΔPTS & ΔPRQ
∠P = ∠P (Common angle)
∠Q = ∠R (PQ = PR)
by AA similarity
ΔPTS ~ ΔPRQ.

Question 13.
Observe the below figure.

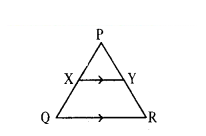
In a ΔPQR, if XY // QR and PX - x - 2, XQ = x + 5, PY = x - 3 and YR = x + 3, then find the value of ‘x’.

Solution:
Given : In ΔPQR, XY // QR and
PX = x - 2, XQ = x + 5, PY = x - 3 and YR = x + 3.
By Basic Proportionality theorem,
If XY // QR then we should have
PX/XQ = PY/YR
∴ x-2/x+5 = x-3/x+3
⇒ (x - 2) (x + 3) = (x - 3) (x + 5)
⇒ x² + 3x - 2x - 6 = x² + 5x - 3x - 15
⇒ x² + x - 6 = x² + 2x- 15
⇒ x - 6 = 2x- 15
⇒ 2x - x = 15 - 6
⇒ x = 9
∴ The value of x = 9 will make
XY // QR.

Question 14.
In a ΔABC, AD ⊥ BC and AD² = BD × CD, prove that ΔABC is a right - angled triangle.

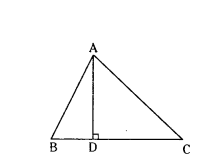
Solution:

Given : In ΔABC, AD ⊥ BC and AD² = BD × CD
RTP : In ΔABC is a right - angled triangle
Proof : AD² = BD × CD
⇒ AD/BD = CD/AD
∠ADB = ∠CDA = 90°
∴ Δ ADB - ΔCDA (∵ S.A.S Similarity)
In Δ ABD, ∠BAD + ∠ABD = 90° (∵ ∠ADB = 90°)
In Δ ACD, ∠DAC + ∠ACD = 90° (∵ ∠ADC = 90°)
∠ BAD = ∠ACD (∵ pair of corresponding angles)
∠ABD = ∠DAC (∵ pair of corresponding angles)
∴ ∠BAD + ∠DAC = 90°
∠BAC = 90°
Δ ABC is a right - angled triangle.

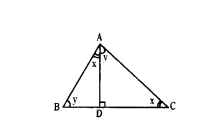
Question 15.
In ΔABC, PQ ‖ BC and AP = 3x - 19, PB = x - 5, AQ = x + 3, QC = 3 cm. Find x.

Solution:
In Δ ABC PQ ‖ BC

⇒ AP/PB = AQ/QC (∵ Basic proportionality theorem)
3x-19/x-5 = x-3/3
9x - 57 = x² - 8x + 15
⇒ x² - 17x + 72 = 0
(x - 8) (x - 9) = 0
x = 8 or x = 9

Question 16.
If the ratio of areas of two equilateral triangles is 25 : 36, then find the ratio of heights of the triangles.

Solution:
For similar triangles
Ratio of area = Ratio of sides

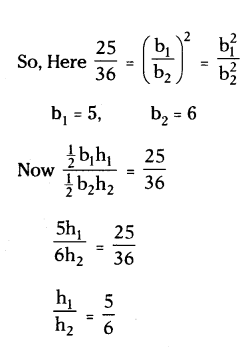
h₁ : h₂ = 5 : 6
∴ The ratio of heights of the triangles = 5 : 6

Question 17.
In ΔABC, D and E are points on AB and AC respectively. If AB = 14 cm; AD = 3.5 cm, AE = 2.5 cm and

AC = 10 cm, show that DE ‖ BC.

Solution:

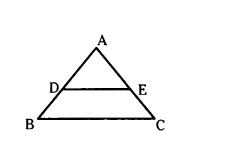
Given AB = 14 cm, AD = 3.5 cm,
AE = 2.5 cm, AC = 10 cm.
BD = AB - AD = 14 - 3.5 = 10.5 cm
EC = AC - AE = 10 - 2.5 = 7.5 cm
AD/DB = 3.5/10.5 = 1/3 .... (1)
AD/DB = 2.5/7.5 = 1/3 ..... (2)
From (1) and (2), AD/DB = AE/EC
∴ DE‖BC (∵ using converse of BPT)

Question 18.
In a rectangle ABCD, AB = 2x - y, BC = 15, CD = 2 and DA = x + 3y, then find the values of x and y.

Solution:
Given that
In a rectangle ΔBCD

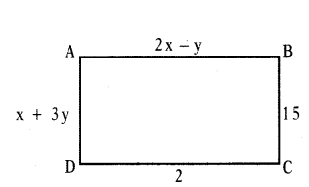
AB = 2x - y
BC = 15; CD = 2; OA = x + 3y
So,
In a rectangle opposite sides are equal
(1) → 2x - y = 2
(2) → x + 3y = 15

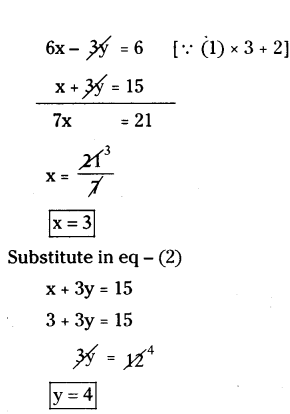
so the value of x is 3 and the value of y is 4.

Question 19.
Observe the below diagram and find the values of x and y.

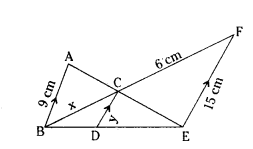
Solution:
ΔABC ~ ΔEFC
x/6 = 9/15 ⇒ x = 9×6/15 = 18/5 = 3.6 cm
ΔBDC ~ ΔBEF
x/9.6 = y/15 ⇒ y = 3.6×15/9.6 = 45/8 = 5.625 cm.

Question 20.
Give two different examples of pair of i) Similar figures, ii) Non - similar
figures.

Solution:
By keeping in view of the definition of similar figures.
(i) Similar figures :
For any two correct examples for similar figures.
(ii) Non similar figures :
For any two correct examples for similar figures.

Question 21.
The hypotenuse of a right triangle is 6m more than twice the shortest side. If the third side is 2m less than hypotenuse, find the sides of the triangle.

Solution:
Let the shortest side = ‘x’ m
then its hypotenuse = (2x + 6) m
Third side = 2x + 6 - 2 = (2x + 4) m
then from Pythagoras theorem, we have

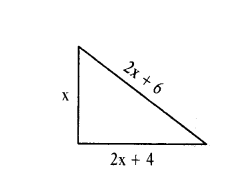
x² + (2x + 4)² = (2x + 6)²
⇒ x² + 4x² + 16x + 16 = 4x² + 24x + 36
⇒ x² + 16x - 24x + 16 - 36 = 0
⇒ x² - 8x - 20 = 0
⇒ x² - 10x + 2x - 20 = 0
⇒ x(x - 10)+ 2(x - 10)= 0
⇒ (x - 10)(x + 2) = 0
⇒ x = 10 or x = -2
but x being the length cannot be negative.
So x ? -2, we consider x = 10 only
then the
shortest side = x = 10 m
third side 2x + 4 = 24m
hypotenuse = 2x + 6 = 26 m

Question 22.
A ladder 25 m long reaches a window of building 24 m above the ground. Determine the distance of the foot of the ladder from the building.

Solution:
In a ΔABC, ∠C = 90°

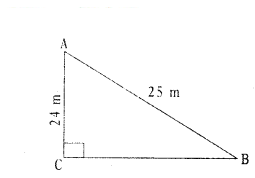
AB = length of ladder = 25m
AC = height of window = 24 m
AB² = AC² + BC²
BC² = AB² - AC²
= 25² - 24² = (25 + 24) (25 - 24)
= 49 × 1 = 7²
∴ BC = 7 m
∴ Distance of the foot of the ladder from the building = 7 m.

Question 23.
In figure EF ‖ AB ‖ DC, prove that AE/ED = BF/FC.

Solution:
Given in ABCD quadrilateral.
EF ‖ AB ‖ DC
In ΔADC, EP ‖ DC.
By Basic Proportionality theorem,
AE/ED = AP/PC → (1)
In ΔCAB, FP ‖ BA.
By Basic Proportionality theorem,
BF/FC = AP/PC → (2)
From (1) and (2) AE/ED = BF/FC.

Question 24.
In figure, DE ‖ BC and CD ‖ EF. Prove that AD² = AB × AF.

Solution:

Given in ΔABC,
DE ‖ BC and CD ‖ EF.
In ΔABC, DE ‖ BC
By Basic Proportionality theorem,
AB/AD = AC/AE → (1)
In ΔADC, FE ‖ DC
By Basic Proportionality theorem,
AD/AF = AC/AE → (2)
From (1) and (2) AB/AD = AD/AF AD.AD = AB.AF
Therefore, AD² = AB.AF.

Question 25.
In a ΔABC, D and E are points on the sides AB and AC respectively such that DE ‖ BC. If AD = 2.5 cm, BD = 3.0 cm and AE = 3.75 cm. Find the length of AC.

Solution:
Given in ΔABC,
AD = 2.5 cm, BD = 3.0 cm and AE = 3.75 cm and DE ‖ BC.
In ΔABC, DE ‖ BC
By Basic Proportionality theorem,

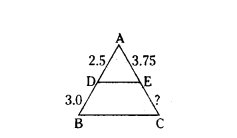
∴ CE = 4.5 cm
AC = AE + CE = 3.75 + 4.5
Therefore, AC = 8.25 cm

Question 26.
If D and E are points on sides AB and AC respectively of a ΔABC such that DE ‖ BC and BD = CE. Prove that ΔABC is isosceles.

Solution:
In ΔABC, DE ‖ BC and BD = CE.
In ΔABC, DE ‖ BC,
By Basic Proportionality theorem,
AD/DB = AE/EC
AD/AE = DB/EC = 1
So, AD/AE = 1

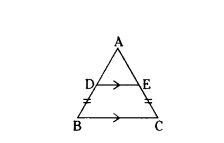
Therefore, AD = AE
So, AD + BD = AE + CE
AB = AC.
In ΔABC, AB = AC
Two sides are equal in ΔABC.
Therefore, ΔABC is an isosceles.

Question 27.
In the given figure AB ‖ CD. If OA = 3x - 19, OB = x - 4, OC = x - 3 and OD = 4, find x.

Solution:
In quadrilateral ABCD, AB ‖ DC.
So, ABCD is a trapezium.
In trapezium diagonals divide each other proportionately.

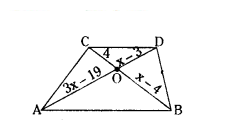
OA/OC = OB/OD
3x-19/x-3 = x-4/4
⇒ 4(3x - 19) = (x - 3) (x - 4)
⇒ 12x - 76 = x² - 4x - 3x + 12
⇒ x² - 7x + 12x + 88 = 0
⇒ x² - 19x + 88 = 0
⇒ x² - 11x - 8x + 88 = 0
⇒ x (x - 11) - 8 (x - 11) = 0
⇒ (x - 8) (x - 11) = 0
Therefore, x = 8 (or) 11.

Question 28.
In figure, QA and PB are perpendiculars to AB. If AO = 10 cm, BO = 6 cm and PB = 9 cm. Find AQ.

Solution:
In ΔAOQ, ΔBOP
∠A = ∠B = 90°
∠AOQ = ∠BOP (Vertically opposite angles)
Angle-Angle criterion of similarity
ΔAOQ ~ ΔBOP.
So, corresponding sides are in proportion.

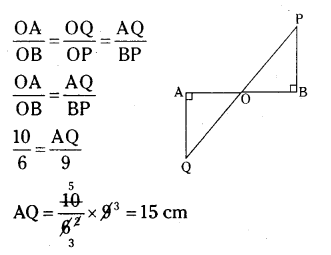
There, AQ = 15 cm.

Question 29.
In figure, considering triangles BEP and CPD. Prove that BP × PD = EP × PC.

Solution:

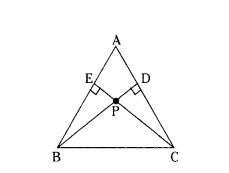
In ΔABC, BD ⊥ AC
and CE ⊥ AB.
In ΔEBP, ΔDCP
∠E = ∠D = 90°
∠EPB = ∠DPC (Vertically opposite angles)
By Angle-Angle criterion similarity
ΔEBP ~ ΔDCP.
So, corresponding sides are in proportion.
BP/PC = EP/PD
Therefore, BP × PD = EP × PC.

Question 30.
In ΔABC, DE ‖ BC, with D on AB and E on AC. If AD/DB = 2/3, find BC/DE.

Solution:
Given in ΔABC.DE ‖ BC and AD/DB = 2/3
In ΔABC, DE ‖ BC.
By Basic Proportionality theorem,

10th Class Maths Triangles 8 Marks Important Questions

Question 1.
In the given figure BE/AC = BC/BD and ∠1 = ∠2. Prove that ΔABD ~ ΔEBC.

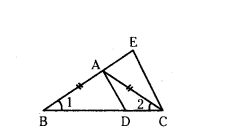
Solution:
Given in ΔBCE,
∠1 = ∠2 and BE/AC = BC/BD
BE/BC = AC/BD → (1)
In ΔMBC, ∠1 = ∠2 and then sides opposite to equal angles are equal.
That is AC = AB → (2)
From (1) and BE/BC = AB/BD
In ΔABD and ΔEBC
∠ABD = ∠EBC = ∠B
and BE/BC = AB/BD
So, by side-angle-side similarity criterion.
Therefore, ΔABD ~ ΔEBC

Question 2.
Given in the trapezium ABCD, AB // DC. If ΔAED ~ ΔBEC then prove that AD = BC.

Solution:

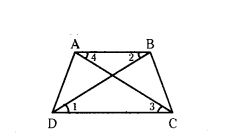
In trapezium ΔBCD, AB // DC and ΔAED ~ ΔBEC. A
In ΔEDC, ΔEBA
∠EDC = ∠EBA
∠1 = ∠2 (Alternate angles)
∠ECD = ∠EAB
∠3 = ∠4 (Alternate angles)
∠CED = ∠AEB (Vertically opposite angles)
By A - A similarity criterion
ΔEDC ~ ΔEBA
Corresponding sides are in proportion
ED/EC = BE/AE → (1)
But,.given ΔAED ~ ΔBEC
then the corresponding sides are in proportion ED/EC = AE/BE = AD/BC → (2)
From (1) and (2)
ED/EC = BE/AE = AE/BE
BE² = AE²
BE = AE ⇒ AE/BE = 1
Put BE = AE in (2)
ED/EC = 1 = AD/BC
AD/BC = 1
Therefore AD = BC.

Question 3.
If a perpendicular is drawn from the vertex containing the right angle of a right triangle to the hypotenuse then prove that the triangle on each side, of the perpendicular are similar to each other and to the original triangle. Also prove that the square of the perpendicular is equal to the product of the length of the two parts of the hypotenuse. That is
i) ΔAOB ~ ΔBOC
ii) ΔADB ~ ΔABC
iii) ΔBOC ~ ΔABC
iv) BD² = AD.DC
v) AB² = AD.AC
vi) BC² = CD.AC

Solution:
Given in ΔABC, ∠B = 90° and BD ⊥ AC
i) ∠ABD + ∠DBC = 90° → (1)
In ΔBOC,
∠BDC + ∠DBC + ∠C = 180°
90° + ∠DBC + ∠C = 180°
∠DBC + ∠C = 180° - 90° = 90° → (2)
From (1) and (2) ∠ABD = ∠C.
In ΔADB, ∠BDC,
∠ABD = ∠C and ∠ADB = ∠BDC = 90°
by Angle-Angle similarity criterion
ΔADB ~ ΔBDC → (3)

ii) In ΔADB and ΔABC
∠ADB = ∠ABC = 90° (Angle)
and ∠A = ∠A (Common angle)
by Angle-Angle similarity criterion.
ΔADB - ΔABC → (4)

iii) In ΔBDC and ΔABC
∠BDC = ∠ABC = 90° (Angle)
∠C = ∠C (Common angle)
By Angle-Angle similarity criterion
ΔBDC ~ ΔABC → (5)
From (3), (4) and (5)
ΔADB ~ ΔBDC ~ ΔBDC - ΔABC

iv) We proved ΔADB ~ ΔBDC then corresponding sides are in proportion
AD/BD = BD/DC
BD.BD = AD.DC
BD² = AD.DC

v) We proved ΔADB ~ ΔABC
AD/AB = AB/AC
AB² = AD.AC

vi) We proved ΔBDC ~ ΔABC
BC/AC = DC/BC
BC² = AC.DC

Question 4.
In ΔABC given AD and BE are perpendiculars to BC and AC respectively show that
i) ΔADC ~ ΔBEC
ii) CA.CE = CB.CD
iii) ΔABC ~ ΔDEC
iv) CD.AB = CA.DE

Solution:
In ΔABC, AD ⊥ BC and BE ⊥ AC

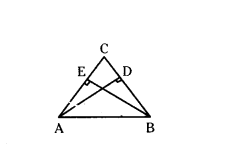
i) In ΔADC and ΔBEC
∠ADC = ∠BEC = 90° (Angle)
∠C = ∠C (Common angle)
By Angle-Angle similarity criterion
ΔADC - ΔBEC

ii) The corresponding sides are in proportion
CA/CB = CD/CE → (1)

iii) In ΔABC, ΔDEC
From(1) AC/BC = DC/EC (or) AC/DC = BC/EC
By Side - Angle - Side similarity criterion ΔABC ~ ΔDEC.

iv) Corresponding sides are in proportion
AB/DE = AC/DC
Therefore, AB.DC = AC.DE

Question 5.
i) State and prove the "Basic Proportionality theorem".
ii) Using the theorem, find the length of AE, if AD = 1.8 cm, BD = 5.4 cm, EC = 7.2 cm.

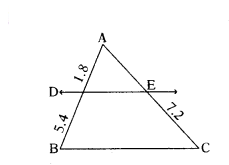
Solution:
i) If a line is drawn parallel to one side of a triangle to intersecting the other two sides, in distinct points, then the other two sides are divided in the sgme ratio.
Given : A triangle ABC in which DE ‖ BC and DE intersects AB in D and AC in E.

To prove: AD/DB = AE/EC

Construction : Join BE, CD and draw EF ⊥ AB, DG ⊥ AC.
Proof : In ΔEAD and ΔEDB, here as EF is perpendicular to AB, therefore, EF is the height for both of triangles EAD and EDB.
Now,
Area of ΔEAD = 1/2 (base × height)
= 1/2 × AD × EF
Area of ΔEDB = 1/2 (base × height)
= 1/2 × DB × EF
Area(ΔEAD)/Area (ΔEDB) = = AD/DB .... (1)
Similarly, Area(ΔEAD)/Area (ΔECD) .... (2)
∵ ΔDBE, ΔECD are on the same base DE and between the same parallels DE ‖ BC, we have
Area of ΔDBE = Area of ΔECD
Hence, (1) = (2)
i.e., AD/DB = AE/EC (Q.E.D).

ii) Using the theorem to find the length of

AD = 1.8 cm, BD = 5.4 cm, EC = 7.2 cm
From the theorem, AD/BD = AE/EC
⇒ AE = (AD)(EC)/BD = 1.8×7.2/5.4 = 2.4
∴ AE = 2.4cm

Question 6.
ABC is a right angled triangle which is right angled at C. Let AB = c, BC = a, CA = b and let p be the length of perpendicular from C on AB. Prove that c = ab/p.

Solution:

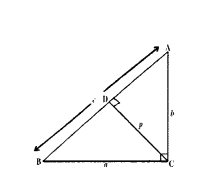
CD ⊥ AB and CD = p.
Also area of ΔABC = 1/2 × AB × CD
= 1/2 cp
Also area of ΔABC = 1/2 × BC × AC
= 1/2 ap
1/2 cp = 1/2 ap ⇒ cp = ap ⇒ c = ab/p

Question 7.
In given figure if PQ ‖ BC and PR ‖ CD. prove that
i)AR/AD = AQ/AB
ii)QB/AQ = DR/AR.

Solution:
In ΔABC, PQ ‖ BC.
By Basic Proportionality theorem,
AQ/AB = AP/AC → (1)
In ΔACD, PR ‖ CD
By Basic Proportionality theorem,
AP/AC = AR/AD → (2)

Question 8.
In a ΔABC, D and E are points on the sides AB and AC respectively such that DE ‖ BC. If AD = 4x - 3, AE = 8x - 7, BD = 3x - 1 and CE = 5x - 3. Find the value of x.

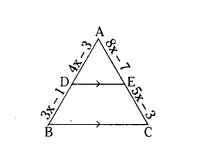
Solution:
In ΔABC, DE ‖ BC
AD = 4x - 3, AE = 8x - 7, BD = 3x - 1 and CE = 5x - 3
In ΔABC, DE ‖ BC
By Basic Proportionality theorem,
AD/BD = AE/CE
⇒ 4x-3/3x-1 = 8x-7/5x-3
⇒ (4x - 3) (5x - 3) = (8x - 7) (3x - 1)
⇒ 20x² - 12x - 15x + 9 = 24x² - 8x - 21x + 7
⇒ - 24x² + 20x² - 27x + 29x + 9 - 7 = 0
⇒ - 4x² + 2x + 2 = 0
⇒ - 2 (2x² - x - 1) = 0
⇒ 2x² - x - 1 = 0
⇒ 2x² - 2x + x - 1 = 0
⇒ 2x(x- 1) + 1 (x- 1) = 0
⇒ (2x + 1) (x - 1) = 0
⇒ 2x + 1 = 0 and x - 1 = 0
x = - 1/2 (or) 1
Length cannot be negative.
Therefore, x = 1

Question 9.
ABCD is a trapezium, in which AB ‖ DC and its diagonals intersect each other at point ‘O’. Show that OA/OB = OC/OD.

Solution:

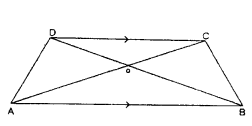
In Δ OAB, Δ OCD
∠AOB = ∠COD (∵ pair of vertically Opp. Angles)
∠OAB = ∠OCD (∵ Pair of alternate angles)
∠OB A = ∠ODC (∵ Pair of alternate angles)
∴ Δ OAB ~ Δ OCD (∵ AAA similarity)
∴ OA/OC = OB/OD ⇒ OA/OB = OC/OD

Question 10.
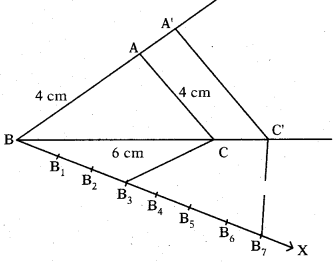
Construct an equilateral triangle XYZ of side 5 cm and construct another triangle similar to ΔXYZ, such that each of its sides is 4/5 of the sides of ΔXYZ.

Solution:

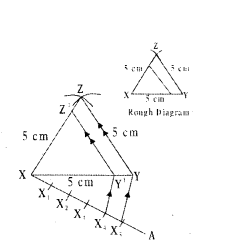
Steps of construction :

Draw an equilateral triangle XYZ with side 5 cm.
Draw a ray XA such that ∠YXA is an acute angle.
Draw X₁, X₂, X₃, X₄, X₅ arcs on XA such that XX₁ = X₁X₂ = ... = X₄X₅
Join X₅ and Y.
Draw a parallel line to X₅Y through X₄ to meet XY at Y’.
Draw a parallel line to YZ through Y’ to meet XZ at Z’.
Δ XY’ Z’ is required similar triangle.

AP 10th Class Maths Important Questions Chapter 6 Similar Triangles

Question 1.
Is a square similar to a rectangle ? Justify your answer.

Solution:
In a square and rectangle, the corresponding angles are equal. But the corresponding sides are not proportional.

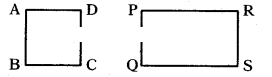
∴ A square and a rectangle are not similar

Question 2.
In ΔABC LM‖BC and AL/LB = 2/3, AM = 5 cm, find AC.

Solution:
In ΔABC, LM // BC

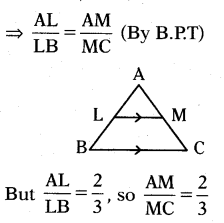
Given AM = 5 cm and AM : MC = 2:3
AM/MC = 2/3 ⇒ 5/MC = 2/3
⇒ MC = 5×3/2 = 15/2 = 7.5
∴ AC = AM + MC = 5 + 7.5 = 12.5 cm

Question 3.

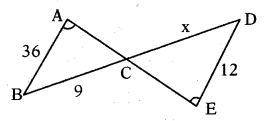
In the figure, ∠BAC = ∠CED, then verify whether the value of ‘x’ is 3 or not.

Solution:
Given: In ΔABC and ΔECD
∠A = ∠E
∠ACB = ∠ECD [∵ Vertically opposite]
∴ LB ¿D [∵ Angle sum property]
∴ ΔABC ~ ΔEDC
⇒ AB/ED = BC/DC = AC/EC ⇒ 36/12 = 9/x
⇒ 36x= 108 ⇒ x= 108/36 = 3

Question 4.
In ΔABC, DE ‖ BC and AC = 5.6 cm, AE = 2.1 cm, then find AD : DB.

Solution:

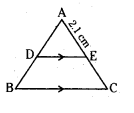
In ΔABC DE ‖ BC,
AE = 2.1 cm
EC = AC - AE
= 5.6 - 2.1 = 3.5 cm
As per B.P.T, AD : DB = AE : EC
= 2.1 : 3.5 = 3:5

Question 5.
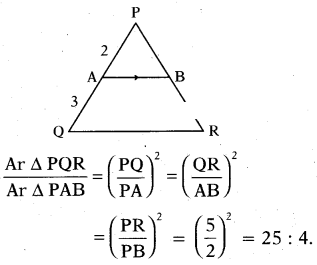
In the given figure, AB‖QR and PA = 2 cm, AQ = 3 cm, then find the ratio of areas of ΔPQR and ΔPAB.

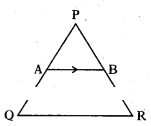
Solution:
Given AB ‖ QR; PA = 2, AQ = 3
then, APQR ~ APAB
∴ PQ = 2 + 3 = 5
∴ Ratio of area of similar triangles is equal to square of ratio of their corre-sponding sides.

Question 6.
Give two different examples of pair of i) Similar figures, ii) Non - similar figures. Mar. ’17
By keeping in view of the definition of similar figures.

Solution:
By keeping in view of the definition of similar figures.
(i) Similar figures :

For any two correct examples for similar figures.
(ii) Non similar figures :

For any two correct examples for non similar figures.

Question 7.
Define A.A. and S.S.S. rules for similarity of two triangles in your own words.

Solution:
A.A. similarity : If two angles of a triangle are equal to two corresponding angles of another triangle, then the two triangles are similar.
S.S.S. similarity : If in two triangles, sides of one triangle are proportional to the sides of other triangle, then their corresponding angles are equal and hence the two triangles are similar.

Question 8.
The hypotenuse of a right triangle is 6m more than twice the shortest side. If the third side is 2m less than hypotenuse, find the sides of the triangle.

Solution:
Let the shortest side = ‘x’m
then its hypotenuse = (2x + 6) m
Third side = 2x + 6 - 2 = (2x + 4) m then from Pythagoras theorem, we have

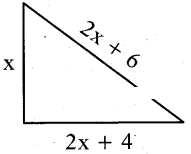
x² + (2x + 4)² = (2x + 6)²
⇒ x² + 4x² + 16x + 16 = 4x² + 24x + 36
⇒ x² + 16x - 24x + 16 - 36 = 0
⇒ x² - 8x - 20 = 0
⇒ x² - 1 Ox + 2x - 20 = 0
⇒ x(x- 10) + 2 (x- 10) = 0
⇒ (x - 10) (x + 2) = 0
⇒ x = 10 or x = -2
but ‘x’ being the length cannot be negative.
So x ? -2, we consider x = 10 only then the
shortest side = x = 10m
third side = 2x + 4 = 24 m
hypotenuse = 2x + 6 = 26m

Question 9.
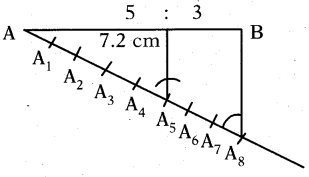
Draw a line segment of length 7.2 cm. and divide it in the ratio 5 : 3 using compasses and ruler.

Solution:

Question 10.
Construct a triangle of sides 4.2 cm, 5.1 cm and 6 cm. Then construct a tri¬angle similar to it, whose sides are 2/3 of corresponding sides of the first tri¬angle.

Solution:

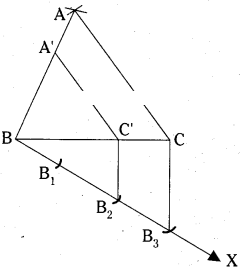
Draw a triangle ABC, with sides AB = 4.2cm,BC = 5.1 cm,CA = 6cm.
Draw a ray BX making an acute angle with BC on the side opposite to vertex A.
Locate 3 points B,, B2, B3 on BX so that BB₁ = B₁B₂ = B₂B₃.
Join B₃,C an draw a line through B₂ parallel to B₃C intersecting BC at C¹.
Draw a line through .C¹ parallel to CA intersect AB at A¹.
A¹BC¹ is required triangle.

Question 11.
Construct a triangle PQR, where QR = 5.5cm,∠Q= 65°andPQ = 6cm. Then draw another triangle, whose sides are 2/3 times of the corresponding sides of ΔPQR.

Solution:
Construction Steps:

Draw a triangle ΔPQR with sides QR = 5.5cm, ∠Q = 65°and PQ = 6cm.
Draw a ray OX making an acute angle with QR on the side opposite to vertex P
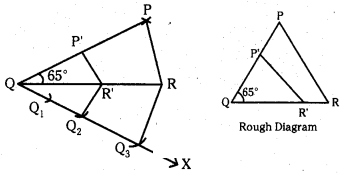
Locate 3 points Q₁ Q₂ Q₃ on QX. So that QQ₁ = Q₁Q₂ = Q₂Q₃
Join Q₃,R and draw a line through Q₂ parallel to Q₃R intersecting QR at R.
Draw a line through ‘R’ parallel to PR intersect PQ at P.
ΔP’QR’ is required triangle.

Question 12.
i) State and prove the "Basic Propor-tionality theorem".
ii) Using the theorem, find the length of AE, if AD = 1.8 cm, BD .= 5.4 cm, EC = 7.2 cm.

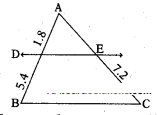
Solution:
If a lines is drawn parallel to one side of a triangle to intersecting the other two sides, in distinct points, then the other two sides are divided in the same ratio.
Given : A triangle ABC in which DE ‖ BC and DE intersects AB in D and AC in E.
To prove : AD/DB=AE/EC

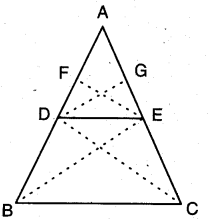
Construction : Join BE, CD and draw EF ⊥ AB, DG ⊥ AC.
Proof : In ∆EAD and ∆EDB, here as EF is perpendicular to AB, therefore, EF is the height for both of triangles EAD and EDB.
Now,
Area of ∆EAD = 1/2 (base x height)
= 1/2 x AD x EF
Area of ∆EDB = 1/2 (base x height)
= 1/2 x DB x EF

∵ ∆DBE, ∆ECD are on the same base DE and between the same parallels DE ‖ BC, we have
Area of ∆DBE = Area of ∆ECD
Hence, (1) = (2)
i.e., AD/DB=AE/EC

ii) Using the theorem, to find the length of AE

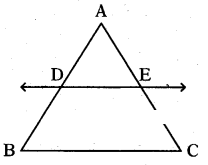
AD = 1.8 cm, BD = 5.4 cm, EC = 7.2 cm
From the theorem, AD/BD = AE/EC
⇒ AE = (AD)(EC)/BD = 1.8×7.2/5.4 = 2.4 cm
∴ AE = 2.4 cm

Question 13.
Draw ΔABC with sides 4.3 cm, 5.2 cm and 6.5 cm and then construct a tri-angle similar to ΔABC, whose sides are 3/5 th of the corresponding sides.

Solution:
Constructing a similar triangle whose sides are 3/5 of corresponding sides.
Steps of construction:
1) Draw a triangle ΔABC with sides AB = 4.3 cm, BC = 5.2 cm and AC = 6.5 cm
2) Draw a ray BX making an acute angle with BC on the side opposite to vertex ‘A’.

3) Locate 5 points B₁; B₂, B₃, B₄, B₅ on the ray BX Such that

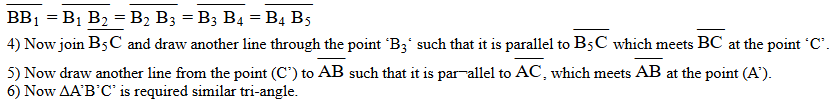
Question 14.
Draw a triangle ABC in which AB = 4 cm, BC = 6 cm and AC = 4 cm. Draw a triangle similar to ΔABC with its sides 3/4 times of the corresponding sides of ΔABC.

Solution:

Question 15.
Divide the line segment AB = 6 cm in the ratio of 3 : 2. Explain the con-struction procedure.

Solution:
Steps to construct:

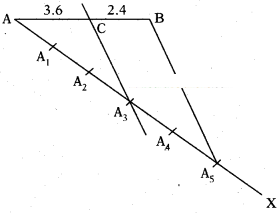
1) Draw a line segment AB = 6 cm
2) Draw a line AX such that ∠BAX is an acute.
3) Make 5 equal parts on AX. (3 + 2)
4) Now join B with last part A₅.
5) Then draw a line from A₃ to AB which meets at ‘C’ such that it is parallel to BA₅.
6) So ‘C’ is the point which divides AB in the ratio of 3 : 2

Question 16.
In the given ΔABC, E and F are two points on AB and AC respectively. Then verify whether EF ‖ BC or not in the following cases.

Solution:
From the converse of Thales theorem
EF ‖ BC if AE/EB=AF/FC

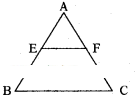
Case I) AE = 3.9, EB = 3,
AF = 3.6, CF = 2.4
Then AE/EB=3.9/3=1.3/1;AF/FC = 3.6/2.4 = 3/2
So AE/EB≠AF/FB then EF ∦ BC
Case II) AE = 4, EB = 4.5;
AF = 8 and CF = 9
So AE/EB=4/4.5=8/9 and AF/FB=8/9
So then AE/EB=AF/FB
hence EF ‖ BC.

Question 17.
In the given figure BC ‖ DE and AD = DB = 3.4 and AC = 14.

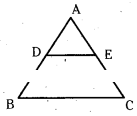
So find AE and EC.

Solution:
In the given ΔABC, DE ‖ BC is given.
So from Thales theorem,
AD/DB=AE/EC
In this problem, AD = DB = 3.4 is given.
And also AC = 14 is given.
So AD/DB=AE/EC
⇒ 3.4/3.4=AE/EC
⇒ AE = EC
But AC = 14 is given.
AC = AE + EC = 2AE = 14
⇒ AE = EC = 7 cm

Question 18.
In given ΔABC points D and E are mid points of AB and AC and also BC = 6 cm then find DE.

Solution:
As shown in the figure D, E are mid points of AB and AC.

Then AD = BD, AE = EC
∴ AD/BD=AE/EC hence DE ‖ BC (From the Converse of Thales theorem)
AD/AB=DE/BC=AE/EC
⇒ AD/2AD=DE/6
⇒ 2DE = 6 and DE = 3 cm
∴ DE = 3 cm

Question 19.
In the given figure, AB ‖ CD ‖ EF given AB = 73cm,DC=ycm,EF 4.5cm, BC = x cm. Calculate the values of x and y.

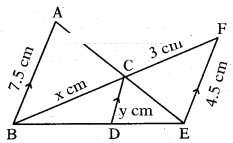
Solution:
Given that, AB ‖ CD ‖ EF and
AB = 7.5 cm, DC = y cm
According to Thales theorem
Δ??CDE ~ Δ??ABE

From (1) and (2)
7.5-y/7.5=y/4.5
7.5 y = (7.5) (4.5)-4.5 y
12y = (7.5) (4.5) = 33.75
y = 33.75/12 = 2.8125
From (2)
y/4.5 = x/x+3; 2.8/4.5 = x/x+3
4.5 x = (2.8) x + 8.4
4.5 x - (2.8) x = 8.4
1.7 x = 8.4
x = 8.4/1.7 = 5 (approx)

Question Papers / Notes Download

Videos

Similar Triangles

Question 1. In △PQR, ST is a line such that PS/SQ=PT/TR and also ∠PST = ∠PRQ. Prove that △PQR is an isosceles triangle.

Question 2. In the given figure, LM ∥ CM and LN ∥ CD. Prove that AMAB = ANAD.

Question 3. In the given figure, DE ∥ AC and DF ∥ AE. Prove that BF/FE = BE/AC.

Question 4. Prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side (Using Basic proportionality theorem).

Question 5. Prove that a line joining the mid points of any two sides of a triangle is parallel to the third side. (Using converse of Basic proportionality theorem)

Question 6. In the given figure, DE ∥ OQ and DF ∥ OR. Show that EF ∥ QR.

Question 7. In the given figure A, B and C are points on OP, OQ and OR respec¬tively such that AB ∥ PQ and AC ∥ PR. Show that BC ∥ QR.

Question 8. ABCD is a trapezium in which AB ∥ DC and its diagonals intersect each other at point ‘O’. Show that AO/BO = CO/DO.

Question 9. Draw a line segment of length 7.2 cm and divide it in the ratio 5 : 3. Measure the two parts. Answer:

Question 1. In the given figure, ∠ADE = ∠B

Question 2. The perimeters of two similar triangles are 30 cm and 20 cm respectively. If one side of the first triangle is 12 cm, determine the corresponding side of the second triangle.

Question 3. A girl of height 90 cm is walking away from the base of a lamp-post at a speed of 1.2 m/sec. If the lamp-post is 3.6 m above the ground, find the length of her shadow after 4 seconds.

Question 4. CM and RN are respectively the medians of similar triangles △ABC and △PQR. Prove that

Question 5. Diagonals AC and BD of a trapezium ABCD with AB ∥ DC intersect each other at the point ‘O’. Using the criterion of similarity for two triangles, show that OA/OC = OB/OD.

Question 6. AB, CD, PQ are perpendicular to BD. AB = x, CD = y and PQ = z, prove that 1/x + 1/y = 1/z.

Question 7. A flag pole 4 m tall casts a 6 m., shadow. At the same time, a nearby building casts a shadow of 24 m. How tall is the building?

Question 8. CD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of △ABC and △FEG respectively. If △ABC ~ △FEG then show that

Question 9. AX and DY are altitudes of two similar triangles △ABC and △DEF. Prove that AX : DY = AB : DE.

Question 10. Construct a triangle shadow similar to the given ?ABC, with its sides equal to 5/3 of the corresponding sides of the triangle ABC.

Question 11. Construct a triangle of sides 4 cm, 5 cm and 6 cm. Then, construct a triangle similar to it,whose sides are 2/3 of the corresponding sides of the first triangle.

Question 12. Construct an isosceles triangle whose base is 8 cm and altitude is 4 cm. Then, draw another triangle whose sides are 1 1/2 times the corresponding sides of the isosceles triangle.

Question 1. Equilateral triangles are drawn on the three sides of a right angled triangle. Show that the area of the triangle on the hypotenuse is equal to the sum of the areas of triangles on the other two sides.

Question 2. Prove that the area of the equilateral triangle described on the side of a square is half the area of the equilateral triangles described on its diagonal.

Question 3. D, E, F are midpoints of sides BC, CA, AB of △ABC. Find the ratio of areas of △DEF and △ABC.

Question 4. In △ABC, XY ‖ AC and XY divides the triangle into two parts of equal area. Find the ratio of AX/XB.

Question 5. Prove that the ratio of areas of two similar triangles is equal to the square of the ratio of their corresponding medians.

Question 6. △ABC ~ △DEF. BC = 3 cm, EF = 4 cm and area of △ABC = 54 cm2. Determine the area of △DEF.

Question 7. ABC is a triangle and PQ is a straight line meeting AB in P and AC in Q. If AP = 1 cm and BP = 3 cm, AQ =1.5 cm, CQ = 4.5 cm. Prove that area of △APQ = 1/16 (area of △ABC).

Question 8. The areas of two similar triangles are 81 cm2and 49 cm2respectively. If the altitude of the bigger triangle is 4.5 cm. Find the corresponding altitude of the smaller triangle.

Question 1. Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals.

Question 2. ABC is a right triangle right angled at B. Let D and E be any points on AB and BC respectively. Prove that AE2+ CD2= AC2+ DE2.

Question 3. Prove that three times the square of any side of an equilateral triangle is equal to four times the square of the altitude.

Question 4. PQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR. Show that PM2 = QM . MR.

Question 5. ABD is a triangle right angled at A and AC ⊥ BD. Show that (i) AB2= BC BD

Question 6. ABC is an isosceles triangle right angled at C. Prove that AB2= 2AC2.

Question 7. ‘O’ is any point in the interior of a triangle ABC. OD ⊥ BC, OE ⊥ AC and OF ⊥ AB, show that

Question 8. A wire attached to vertical pole of height 18 m is 24 m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?

Question 9. Two poles of heights 6 m and 11m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.

Question 10. In an equilateral triangle ABC, D is a point on side BC such that BD = 1/3 BC. Prove that 9AD2 = 7AB2.

Question 11. In the given figure, ABC is a triangle right angled at B. D and E are points on BC trisect it. Prove that 8 AE2= 3 AC2+ 5 AD2.

Question 12. ABC is an isosceles triangle right angled at B. Equilateral triangles ACD and ABE are constructed on sides AC and AB. Find the ratio between the areas of △ABE and △ACD.

6th Lesson Triangles Class 10 Important Questions with Solutions

10th Class Maths Triangles 1 Mark Important Questions

Question 1. Write the properties of similar triangles.

Question 2. Write the examples of similar figures.

Question 3. State the Thales theorem.

Question 4. State the converse of basic proportionality theorem.

Question 5. State the pythagoras theorem.

Question 6. In ΔABC and ΔDEF, AB/DE = BC/FD. Which of the following makes the two triangles similar ?

Question 7. In the given fig. DE ‖ BC. Find BC.

Question 8. In ΔABC, PQ ‖ BC. If PB = 6 cm, AP = 4 cm, AQ = 8 cm, find the length of AC.

Question 9. In the given figure, ΔABC ~ ΔQPR, If AC = 6 cm, BC = 5 cm, QR = 3 cm and PR = x; then the value of x is :

Question 10. If in ΔABC and ΔPQR, AB/QR = BC/PR = CA/PQ then : A) ΔPQR ~ ΔCAB B) ΔPQR ~ ΔABC A) ΔCBA ~ ΔPQR B) ΔBCA ~ ΔPQR

Question 11. Which of the following is not a similarity criterion of triangle ? A) AA B) SAS C) AAA D) RHS

Question 12. If ΔABC, AB = 6√3 cm, AC = 12 cm and BC = 6 cm, then ∠B = ..... .

Question 13. In the given fig. DE ‖ BC. Which of the following is true ?

Question 14. In ΔABC and ΔDEF, ∠F = ∠C, ∠B = ∠E and AB = 1/2 DE then the two triangles are

Question 15. In the given fig. If DE ‖ BC. Find EC.

Question 16. In the given figure, AD = 2 cm, DB = 3 cm, DE = 2.5 cm and DE ‖ BC. Find the value of x.

Question 17. In two triangles ΔPQR and ΔABC, it is given that AB/BC = PQ/PR For these two triangles to be similar, which of the following should be true ?

Question 18. In ΔABC, DE ‖ BC, AD = 4 cm, BD = 6 cm and AE = 5 cm, find the length of EC.

Question 19. In ΔABC, DE ‖ BC, AD = 2 cm, BD = 3 cm, DE: BC is equal to ...... .

Question 20. In the given fig. DE ‖ BC. If AD = 3 cm, AB = 7 cm and EC = 3 cm, then find the length of AE.

Question 21. The perimeters of two similar triangles are 24 cm and 18 cm respectively. If one side of the first triangle is 8 cm then what is the corresponding side of second triangle ?

Question 22. In ΔABC, ∠B = 90°, BD ⊥ AC. If AD = 8 cm and BD = 4 cm, then what is the length of CD ?

Question 23. Among "Circles", "Squares" and "Triangles", which are always similar ?

Question 24. In ΔABC and ΔDEF, if ∠B = ∠E, ∠C = ∠F, then which of the following is a true statement ?

Question 25. Given DE ‖ BC, AD = 4.5 cm, BD = 9 cm, and EC = 8 cm. What is the length of AE?

Question 26. The sides of two equilateral triangles ABC and DEF are 4 cm. and 5 cm. respeclively. Find ar(△DEF)/ar(△ABC).

Question 27. ΔABC ~ ΔDEF and ∠A = ∠D = 90°, find the measure of ∠B + ∠F.

Question 28. Given AB ‖ CD, identify the pair of similar triangles in this image and justify.

Question 29. ABC is a triangle in which

Question 30. Statement-I: The lengths 3 cm, 4 cm, 5 cm form a right angled triangle. Statement-II: If ‘a’ is the side of an equilateral triangle, then its height is √3 a. Now, choose the correct answer.

Question 31. Give two different examples of pair of similar figures.

Question 32. "In a right triangle, the square of hypotenuse is equal to the sum of the squares of the other two sides." The above theorem is related to which Mathematician ?

Question 33. Assertion (A) : The sides of two similar triangles are in the ratio 2 : 5, then the areas of these triangles are in the ratio 4 : 25 Reason (R) : The ratio of the areas of two similar triangles is equal to the square of the ratio of their sides.

10th Class Maths Triangles 2 Marks Important Questions

Question 1. In the figure, if RS // ID then find AR.

Question 2. In ΔABC, D and E are point on the sides of AB and AC respectively. Such that DE // BC. If AD/DB = 2/3 and AC = 18 cm, find AE.

Question 1.
In △PQR, ST is a line such that PS/SQ=PT/TR and also ∠PST = ∠PRQ.
Prove that △PQR is an isosceles triangle.

Question 2.
In the given figure, LM ∥ CM and LN ∥ CD. Prove that AMAB = ANAD.

Question 3.
In the given figure, DE ∥ AC and DF ∥ AE. Prove that BF/FE = BE/AC.

Question 4.
Prove that a line drawn through the mid-point of one side of a triangle parallel to another side bisects the third side (Using Basic proportionality theorem).

Question 5.
Prove that a line joining the mid points of any two sides of a triangle is parallel to the third side. (Using converse of Basic proportionality theorem)

Question 6.
In the given figure, DE ∥ OQ and DF ∥ OR. Show that EF ∥ QR.

Question 7.
In the given figure A, B and C are points on OP, OQ and OR respec¬tively such that AB ∥ PQ and AC ∥ PR. Show that BC ∥ QR.

Question 8.
ABCD is a trapezium in which AB ∥ DC and its diagonals intersect each other at point ‘O’. Show that AO/BO = CO/DO.

Question 9.
Draw a line segment of length 7.2 cm and divide it in the ratio 5 : 3. Measure the two parts.
Answer:

Question 1.
In the given figure, ∠ADE = ∠B

Question 2.
The perimeters of two similar triangles are 30 cm and 20 cm respectively. If one side of the first triangle is 12 cm, determine the corresponding side of the second triangle.

Question 3.
A girl of height 90 cm is walking away from the base of a lamp-post at a speed of 1.2 m/sec. If the lamp-post is 3.6 m above the ground, find the length of her shadow after 4 seconds.

Question 4.
CM and RN are respectively the medians of similar triangles △ABC and △PQR. Prove that

Question 5.
Diagonals AC and BD of a trapezium ABCD with AB ∥ DC intersect each other at the point ‘O’. Using the criterion of similarity for two triangles, show that OA/OC = OB/OD.

Question 6.
AB, CD, PQ are perpendicular to BD. AB = x, CD = y and PQ = z, prove that 1/x + 1/y = 1/z.

Question 7.
A flag pole 4 m tall casts a 6 m., shadow. At the same time, a nearby building casts a shadow of 24 m. How tall is the building?

Question 8.
CD and GH are respectively the bisectors of ∠ACB and ∠EGF such that D and H lie on sides AB and FE of △ABC and △FEG respectively. If △ABC ~ △FEG then show that

Question 9.
AX and DY are altitudes of two similar triangles △ABC and △DEF. Prove that AX : DY = AB : DE.

Question 10.
Construct a triangle shadow similar to the given ?ABC, with its sides equal to 5/3 of the corresponding sides of the triangle ABC.

Question 11.
Construct a triangle of sides 4 cm, 5 cm and 6 cm. Then, construct a triangle similar to it,whose sides are 2/3 of the corresponding sides of the first triangle.

Question 12.
Construct an isosceles triangle whose base is 8 cm and altitude is 4 cm. Then, draw another triangle whose sides are 1 1/2 times the corresponding sides of the isosceles triangle.

Question 1.
Equilateral triangles are drawn on the three sides of a right angled triangle. Show that the area of the triangle on the hypotenuse is equal to the sum of the areas of triangles on the other two sides.

Question 2.
Prove that the area of the equilateral triangle described on the side of a square is half the area of the equilateral triangles described on its diagonal.

Question 3.
D, E, F are midpoints of sides BC, CA, AB of △ABC. Find the ratio of areas of △DEF and △ABC.

Question 4.
In △ABC, XY ‖ AC and XY divides the triangle into two parts of equal area. Find the ratio of AX/XB.

Question 5.
Prove that the ratio of areas of two similar triangles is equal to the square of the ratio of their corresponding medians.

Question 6.
△ABC ~ △DEF. BC = 3 cm, EF = 4 cm and area of △ABC = 54 cm². Determine the area of △DEF.

Question 7.
ABC is a triangle and PQ is a straight line meeting AB in P and AC in Q. If AP = 1 cm and BP = 3 cm, AQ =1.5 cm, CQ = 4.5 cm. Prove that area of △APQ = 1/16 (area of △ABC).

Question 8.
The areas of two similar triangles are 81 cm²and 49 cm²respectively. If the altitude of the bigger triangle is 4.5 cm. Find the corresponding altitude of the smaller triangle.

Question 1.
Prove that the sum of the squares of the sides of a rhombus is equal to the sum of the squares of its diagonals.

Question 2.
ABC is a right triangle right angled at B. Let D and E be any points on AB and BC respectively. Prove that AE²+ CD²= AC²+ DE².

Question 3.
Prove that three times the square of any side of an equilateral triangle is equal to four times the square of the altitude.

Question 4.
PQR is a triangle right angled at P and M is a point on QR such that PM ⊥ QR. Show that PM² = QM . MR.

Question 5.
ABD is a triangle right angled at A and AC ⊥ BD.
Show that (i) AB²= BC BD

Question 6.
ABC is an isosceles triangle right angled at C. Prove that AB²= 2AC².

Question 7.
‘O’ is any point in the interior of a triangle ABC.
OD ⊥ BC, OE ⊥ AC and OF ⊥ AB, show that

Question 8.
A wire attached to vertical pole of height 18 m is 24 m long and has a stake attached to the other end. How far from the base of the pole should the stake be driven so that the wire will be taut?

Question 9.
Two poles of heights 6 m and 11m stand on a plane ground. If the distance between the feet of the poles is 12 m, find the distance between their tops.

Question 10.
In an equilateral triangle ABC, D is a point on side BC such that BD = 1/3 BC. Prove that 9AD² = 7AB².

Question 11.
In the given figure, ABC is a triangle right angled at B. D and E are points on BC trisect it. Prove that 8 AE²= 3 AC²+ 5 AD².

Question 12.
ABC is an isosceles triangle right angled at B. Equilateral triangles ACD and ABE are constructed on sides AC and AB. Find the ratio between the areas of △ABE and △ACD.

Question 1.
Write the properties of similar triangles.

Question 2.
Write the examples of similar figures.

Question 3.
State the Thales theorem.

Question 4.
State the converse of basic proportionality theorem.

Question 5.
State the pythagoras theorem.

Question 6.
In ΔABC and ΔDEF, AB/DE = BC/FD. Which of the following makes the two triangles similar ?

Question 7.
In the given fig. DE ‖ BC. Find BC.

Question 8.
In ΔABC, PQ ‖ BC. If PB = 6 cm, AP = 4 cm, AQ = 8 cm, find the length of AC.

Question 9.

In the given figure, ΔABC ~ ΔQPR, If AC = 6 cm, BC = 5 cm, QR = 3 cm and PR = x; then the value of x is :

Question 10.
If in ΔABC and ΔPQR, AB/QR = BC/PR = CA/PQ then :
A) ΔPQR ~ ΔCAB
B) ΔPQR ~ ΔABC
A) ΔCBA ~ ΔPQR
B) ΔBCA ~ ΔPQR

Question 11.
Which of the following is not a similarity criterion of triangle ?
A) AA
B) SAS
C) AAA
D) RHS

Question 12.
If ΔABC, AB = 6√3 cm, AC = 12 cm and BC = 6 cm, then ∠B = ..... .

Question 13.
In the given fig. DE ‖ BC. Which of the following is true ?

Question 14.
In ΔABC and ΔDEF, ∠F = ∠C, ∠B = ∠E and AB = 1/2 DE then the two triangles are

Question 15.
In the given fig. If DE ‖ BC. Find EC.

Question 16.
In the given figure, AD = 2 cm, DB = 3 cm, DE = 2.5 cm and DE ‖ BC. Find the value of x.

Question 17.
In two triangles ΔPQR and ΔABC, it is given that AB/BC = PQ/PR For these two triangles to be similar, which of the following should be true ?

Question 18.
In ΔABC, DE ‖ BC, AD = 4 cm, BD = 6 cm and AE = 5 cm, find the length of EC.

Question 19.
In ΔABC, DE ‖ BC, AD = 2 cm, BD = 3 cm, DE: BC is equal to ...... .

Question 20.
In the given fig. DE ‖ BC. If AD = 3 cm, AB = 7 cm and EC = 3 cm, then find the length of AE.

Question 21.
The perimeters of two similar triangles are 24 cm and 18 cm respectively. If one side of the first triangle is 8 cm then what is the corresponding side of second triangle ?

Question 22.
In ΔABC, ∠B = 90°, BD ⊥ AC.
If AD = 8 cm and BD = 4 cm, then what is the length of CD ?

Question 23.
Among "Circles", "Squares" and "Triangles", which are always similar ?

Question 24.
In ΔABC and ΔDEF,
if ∠B = ∠E, ∠C = ∠F, then which of the following is a true statement ?

Question 25.
Given DE ‖ BC, AD = 4.5 cm, BD = 9 cm, and EC = 8 cm. What is the length of AE?

Question 26.
The sides of two equilateral triangles ABC and DEF are 4 cm. and 5 cm. respeclively. Find ar(△DEF)/ar(△ABC).

Question 27.
ΔABC ~ ΔDEF and ∠A = ∠D = 90°, find the measure of ∠B + ∠F.

Question 28.
Given AB ‖ CD, identify the pair of similar triangles in this image and justify.

Question 29.
ABC is a triangle in which

Question 30.
Statement-I: The lengths 3 cm, 4 cm, 5 cm form a right angled triangle. Statement-II: If ‘a’ is the side of an equilateral triangle, then its height is √3 a. Now, choose the correct answer.

Question 31.
Give two different examples of pair of similar figures.

Question 32.
"In a right triangle, the square of hypotenuse is equal to the sum of the squares of the other two sides." The above theorem is related to which Mathematician ?

Question 33.
Assertion (A) : The sides of two similar triangles are in the ratio 2 : 5, then the areas of these triangles are in the ratio 4 : 25
Reason (R) : The ratio of the areas of two similar triangles is equal to the square of the ratio of their sides.

Question 1.
In the figure, if RS // ID then find AR.

Question 2.
In ΔABC, D and E are point on the sides of AB and AC respectively. Such that DE // BC. If AD/DB = 2/3 and AC = 18 cm, find AE.

Question 3.
In the figure, if AB ⊥ BC and DE ⊥ AC. Prove that ΔABC ~ ΔAED.

Question 4.
A vertical stick 10 cm long casts a shadow 8 cm long. At the same time a tower casts a shadow 30 m long. Determine the height of the tower.

Question 5.
A vertical stick of length 6 m casts a shadow 4 m long on the ground and at the same time a tower casts the shadow 28 m long. Find the height of the tower.

Question 6.
The perimeter of two similar triangles ABC and PQR are respectively 36 cm and 24 cm. If PQ = 10 cm find AB.